Движение манипулятора осуществляется от приводов, которые могут располагаться на подвижных звеньях или на неподвижном основании. Число приводных двигателей обычно равно числу степеней свободы манипулятора, хотя во время выполнения технологических операций на систему могут накладываться дополнительные связи.

Передача движения от двигателей к звеньям механизма осуществляется с помощью передаточных механизмов различного вида. Система передаточных механизмов в случае расположения приводов на основании может быть достаточно сложной.

Если не учитывать переда­точные механизмы, то манипу­лятор представляет собой не­замкнутую кинематическую цепь. Высокие требования по быстродействию и точности приводят к необходимости учитывать упругость звеньев основного и передаточных механизмов промышленного робота. Следует иметь в виду, что при анализе динамики манипуляторов недостаточно использовать хорошо развитые методы колебаний упругих систем с постоянными пара­метрами, а необходимо рассматривать задачу движения упругих тел, сопровождающегося колебаниями.

Манипулятором называется техническое устройство, предназначенное для воспроизведения некоторых рабочих функций рук человека. Манипулятором называют также исполнительный механизм промышленного робота, оснащен­ный приводами и рабочим органом, с помощью которого осуществляется выполнение рабочих функций. Способность воспроизводить движения, подобные движениям рук человека, достигается приданием манипулятору нескольких степеней свободы, по которым осуществляется управляемое движение с целью получения заданного движения рабочего органа - схвата.

Числом степеней свободы механической системы называется число возможных перемещений системы.

С точки зрения механики манипулятор представляет систему твердых и упругих тел, связанных между собой посредством соединений с различными видами связей. С точки зрения теории механизмов манипулятор являет­ся системой тел, предназначенных для преобразования движений нескольких тел в требуемые движения других тел, т. е. с этой точки зрения манипулятор представляет собой пространственный механизм с несколькими степеня­ми свободы.

Твердые тела, входящие в механическую систему мани­пулятора, называются звеньями. В механике различают входные и выходные звенья. Входным называется звено, которому сообщается движение, преобразуемое механиз­мом. Выходным называется звено, совершающее рабо­чее движение. Таким образом, в манипуляторе число входных звеньев равно числу приводов, а выходное звено, как правило, одно - схват, или рабочий орган.

Подвижное соединение двух соприкасающихся звеньев называется кинематической парой. Кинематические пары могут быть классифицированы как по числу степеней свободы звеньев в их относи­тельном движении, так и по числу связей, налагаемых парой на относительное движение звеньев. По первому признаку различают одно-, двух-, трех-, четырех-, пяти-подвижные кинематические пары. По второму признаку — кинематические пары пятого, четвертого, третьего, второго и первого класса (классификация И. И. Артоболевского). В манипуляторах в основном получили распространение одноподвижные кинематические пары, т. е. пары пятого класса, допускающие относительное вращательное, поступа­тельное или винтовое движение.

Совокупность звеньев, образующих между собой кине­матические пары, называется кинематической цепью. Кинематические цепи подразделяются на плоские и пространственные в зависимости от вида движения звеньев: в одной или нескольких параллельных плоскостях и в пространстве.

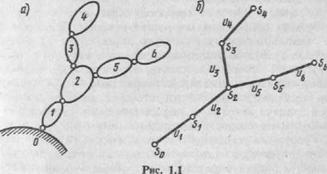
Кинематические цепи могут быть замкнутыми или незамкнутыми. Незамкнутой кинематической цепью называют такую цепь, в которой есть звенья, входящие в одну кинематическую пару.

Часто говорят, что манипуляторы имеют незамкнутую кинематическую цепь, однако это не всегда так. Для приведения в движение манипулятор по каждой степени свободы обычно снабжается отдельным приводом и механиз­мом, имеющим замкнутую кинематическую цепь. Поэтому весь манипулятор представляет собой наслоение замкнутых механизмов с одной степенью свободы.

Однако в манипуляторе часто можно выделить основной механизм с несколькими степенями свободы и, пренебрегая звеньями приводных механизмов, говорить о наличии незамкнутой кинематической цепи. Этот основной механизм отражает основные кинематические и динами­ческие свойства манипулятора как системы с несколькими степенями свободы.

Число степеней свободы манипулятора равно числу обобщенных координат, под которыми понимают независимые переменные, однозначно определяющие положе­ние манипулятора в пространстве.

Кинематические пары накладывают ограничения как на относительное, так и на абсолютное движение звеньев. Связи могут накладываться на манипулятор также в про­цессе выполнения рабочих операций.

Связи могут быть выражены уравнениями или неравен­ствами, связывающими координаты и их производные по времени. Связи называются кинематическими или дифференциальными, если они устанавливают связь между координатами и их производными по времени.

3. Критерии эффективности проектирования систем управления. Принятие решений на основе матрицы эффективности. Обобщенный критерий эффективности проектирования систем управления.

Под эффективностью понимается мера оценка успешности процесса проектирования. Эффективность количественно оценивают показателями или критериями эффективности.

В качестве критериев эффективности при проектировании систем управления используются: вероятность совершения какого-либо события (например, выполнение в данный срок проектных работ или обеспечение заданных технических характеристик системы управления и другие); математическое ожидание некоторой случайной величины. Конкретный вид критерия эффективности W выбирают в зависимости от поставленной задачи. При этом выделяют два класса задач: достижение заданного результата (эффекта), который может быть получен или не получен; достижение наилучшего значения некоторой величины, оценивающей конечный результат процесса.

Для задач первого класса критерий эффективности

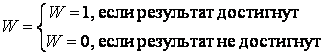(4.22) а для задач второго класса

(4.23) или

(4.24)

При вероятностной модели, когда достижение заданного результата является случайным событием, то

, (4.25) где событие А осуществляется мерилом: выполнено-не выполнено или

, (4.26) где – математическое ожидание оптимизируемой величины (например, максимум точности системы).

На практики часто наблюдается ситуация, когда условия прохождения процесса проектирования системы управления заранее не известны и могут изменяться. Здесь решение может быть найдено сравнением по величине критериев эффективности нескольких вариантов решений в диапазоне условий , , …, .