Если такая функция существует, она называется плотностью совместного распределения случайных величин ξ1, ξ2.

Замечание 14. Для всего дальнейшего более чем достаточно считать, что

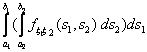
равняется объему под графиком функции f над областью интегрирования — прямоугольником [a1,b1] x [a2,b2].

Плотность совместного распределения обладает свойствами, аналогичными свойствам плотности распределения одной случайной величины:

(f1) для любых x1, x2 Î R;

(f2) .

Более того, любая функция, обладающая этими свойствами, является плотностью некоторого совместного распределения.

Если совместное распределение абсолютно непрерывно, то по функции совместного распределения его плотность находится как смешанная частная производная:

(f3) .

Из свойства (F2) функции совместного распределения вытекает следующее утверждение. Для n > 2 это утверждение, как и свойство (F2), выглядит существенно иначе!

Теорема 22. Если случайные величины ξ1, ξ2 имеют абсолютно непрерывное совместное распределение с плотностью f (x1, x2), то ξ1, и ξ2 в отдельности также имеют абсолютно непрерывное распределение с плотностями:

9.3 Независимость случайных величин

Определение 33. Случайные величины ξ1, ξ2, … , ξn независимы, если для любого набора множеств В1 Í R, … Вn Í R имеет место равенство:

Это определение можно сформулировать в терминах функций распределения:

Определение 34. Случайные величины ξ1, ξ2, … , ξn независимы, если для любых х1, х2, … , хn имеет место равенство:

Определение 35. Случайные величины ξ1, ξ2, … , ξn с дискретным распределением независимы, если для любых а1, а2, … , аn имеет место равенство:

Для случайных величин с абсолютно непрерывным совместным распределением определение независимости можно сформулировать так:

Определение 36. Случайные величины ξ1, ξ2, … , ξn с абсолютно непрерывным совместным распределением независимы, если плотность совместного распределения равна произведению плотностей случайных ξ1, ξ2, … , ξn, то есть для любых х1, х2, … , хn имеет место равенство:

Раздел 10. Преобразования случайных величин

10.1 Преобразование одной случайной величины

Мы будем рассматривать только преобразования случайных величин с абсолютно непрерывными распределениями. Пусть с. в. ξ имеет функцию распределения Fξ(x) и плотность распределения fξ(x). Построим с помощью функции g: R ® R случайную величину η=g(ξ). Требуется найти функцию распределения и, если существует, плотность распределения η.

Замечание 15. Плотность распределения случайной величины η=g(ξ) существует далеко не при любых функциях g. Так, если функция g кусочно-постоянна, то с. в. η имеет дискретное распределение, и плотность ее распределения не существует.

Плотность распределения g(ξ) заведомо существует, если, например, функция g(ξ) монотонна («строго монотонна»). Вспомним, что означает «найти плотность распределения η, если она существует».

По определению, если мы представим (для любого х) функцию распределения η в виде где подинтегральная функция h(y) неотрицательна, то плотность распределения с.в. η существует и в точности равна подинтегральной функции fξ(x) = h(x) .

Так что доказывать существование плотности распределения и находить ее мы будем одновременно, находя нужное интегральное представление для функции распределения.

Теорема 23. Пусть ξ имеет функцию распределения Fξ(x) и плотность распределения fξ(x) , и постоянная a отлична от нуля. Тогда случайная величина η = a ξ + b имеет плотность распределения

Для произвольной монотонной функции g (то есть либо монотонно возрастающей функции, либо монотонно убывающей функции справедливо аналогичное теореме 23 утверждение).

Теорема 24. Пусть ξ имеет функцию распределения Fξ(x) и плотность распределения fξ(x), и функция g: R ® R монотонна. Тогда случайная величина η=g(ξ) имеет плотность распределения

Здесь g -1— функция, обратная к g, и

— производная функции g -1.

Следствие 7. Если ξ Î N0,1, то η = σξ+а Î

Следствие 8. Если η Î , то ξ = (η –а)/ σ Î N0,1.

Следствие 9. Если ξ Î Еα, то η = αξÎ Е1

10.2 Функции от двух случайных величин

Пусть ξ1 ξ2 — случайные величины с плотностью совместного распределения , и задана функция g: R2 ® R. Требуется найти функцию (а если существует, то и плотность) распределения случайной величины η = g(ξ1 , ξ2).

Пользуясь тем, что вероятность случайному вектору попасть в область можно вычислить как объем под графиком плотности распределения вектора над этой областью, сформулируем утверждение.

Теорема 25. Пусть хÎ R, и область Dx Î R2 состоит из точек (x1 x2 ) таких, что g (x1 x2 ) < x. Тогда случайная величина η = g(ξ1 , ξ2). имеет функцию распределения

Всюду далее в этой главе предполагается, что случайные величины ξ1 и ξ2 независимы, то есть