Все остальные благоприятные исходы отличаются лишь расположением чисел 1, 2, …m на n местах. Число таких исходов равно числу способов расставить на n местах n1 единиц, n2 двоек, , … , nm раз чисел m, то есть

Теперь мы можем вернуться к примеру 20(б) и выписать ответ: так как вероятности выпадения шестерки и единицы равны 1/6, а вероятность третьего исхода (выпали любые другие грани) равна 4/6, то вероятность получить 10 шестерок, 3 единицы и еще 2 других очка равна

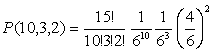
5.6 Теорема Пуассона для схемы Бернулли

Предположим, нам нужна вероятность получить не менее десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003. Вероятность этого события равна любому из следующих выражений:

и вычисление даже одного слагаемого в каждом из этих выражений весьма проблематично.

Сформулируем теорему о приближенном вычислении вероятности какого-либо числа успехов в большом числе испытаний схемы Бернулли с маленькой вероятностью успеха. Термин «большое число» должен означать n → ∞. Если при этом p = pn→ 0,то, очевидно, вероятность получить любое конечное число успехов при растущем числе испытаний стремится к нулю. Необходимо чтобы вероятность успеха p = pn→ 0 одновременно с ростом числа испытаний. Но от испытания к испытанию вероятность успеха меняться не может (см. определение схемы Бернулли).

Поэтому рассмотрим «схему серий»: есть

одно испытание ○ с вероятностью успеха p1

два испытания ○ , ○ с вероятностью успеха p2

…

n испытаний ○ , … , ○ с вероятностью успеха pn

…

Вероятность успеха меняется не внутри одной серии испытаний, а от серии к серии, когда меняется общее число испытаний. Обозначим через vn число успехов в n-той серии испытаний.

Теорема 17 (Теорема Пуассона).

Пусть n → ∞ , pn→ 0 так, что n pn→ λ > 0. Тогда для любого k ≥ 0 вероятность получить k успехов в n испытаниях схемы Бернулли с вероятностью успеха pn стремится к величине

(5)

для n → ∞ , pn→ 0 так, что n pn→ λ

Определение 22. Пусть λ > 0— некоторая постоянная. Набор чисел называется распределением Пуассона с параметром λ.

Пользуясь теоремой 17, можно приближенно посчитать вероятность получить не менее десяти успехов в 1000 испытаний схемы Бернулли с вероятностью успеха 0.003, с вычисления которой мы начали. Поскольку n = 1000 «велико», а pn = 0.003 «мало», то, взяв λ = n pn = 3 , можно написать приближенное равенство

(6)

Осталось решить, а достаточно ли n=103 «велико», а pn = 0.003 «мало», чтобы заменить точную вероятность P(vn = k) на приближенное значение

Для этого нужно уметь оценивать разницу между этими двумя вероятностями.

Теорема 18 (Теорема Пуассона с оценкой погрешности).

Пусть A Í {0, 1, …, n} — произвольное множество целых неотрицательных чисел, vn — число успехов в n испытаниях схемы Бернулли с вероятностью успеха p, λ = n p. Тогда

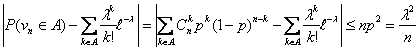
Таким образом, теорема 18 предоставляет нам возможность самим решать, достаточно ли n «велико», а p «мало», руководствуясь полученной величиной погрешности.

Какова же погрешность в формуле (6)?

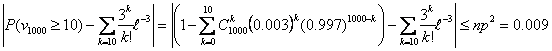
Погрешность не более 0,009 (при вероятности около 0,001). Во всяком случае, можно утверждать, что искомая вероятность никак не больше, чем 0,01=0,001+0,009.

Рассмотрим еще одну формулу приближенного вычисления pn (m) когда n велико. В отличии от предыдущего результата число успехов m в этом случае тоже растет с ростом n, а вероятность успеха постоянна.

Локальная теорема Муавра – Лапласа

Пусть .Предположим, что и величины являются ограниченными. Тогда

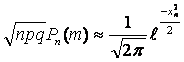
В частности, если , то

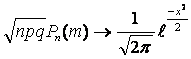
Доказательство:

В силу ограниченности величин разность вместе с n и m Воспользуемся формулой Стирлинга

В силу определения

Раздел 6. Случайные величины и их распределения

6.1 Случайные величины

Мы уже видели, что для очень многих экспериментов нет никаких различий в подсчете вероятностей событий, тогда как элементарные исходы в этих экспериментах очень различаются. Но нас и должны интересовать именно вероятности событий, а не структура пространства элементарных исходов. Поэтому пора во всех таких «похожих» экспериментах вместо самых разных элементарных исходов использовать, например, числа. То есть ввести соответствие (иначе говоря, отображение) между элементарными исходами и вещественными числами (с ними удобно работать).

Пусть имеется случайный эксперимент и задано вероятностное пространство (Ω, Ψ,Р).

Определение 23. Функция ξ: Ω →R называется случайной величиной, если для любого х Î R множество { ξ < x} = {ω: ξ(ω) < x} является событием, то есть принадлежит σ-алгебре событий Ψ.

Замечание 10. Можно смело считать, что любое множество элементарных исходов есть событие, и, следовательно, случайная величина есть произвольная функция из Ω в R. Никаких неприятностей на практике это обычно не влечет.

Определение 24. Будем говорить, что функция ξ: Ω →R является Ψ -измеримой, если {ω: ξ(ω) < x} принадлежит Ψ для любого х Î R.

Итак, случайная величина есть Ψ - измеримая функция, ставящая в соответствие каждому элементарному исходу ω Î Ω число ξ(ω) Î R.