F3) Функция распределения Fξ(x) непрерывна слева:

Теорема 20. Если функция F: R ® [0, 1] удовлетворяет свойствам (F1)–(F3), то F есть функция распределения некоторой случайной величины ξ, то есть найдется вероятностное пространство (Ω, Ψ, Р) и случайная величина ξ на этом пространстве, что F(х) = Fξ(x).

Прочие полезные свойства функций распределения

F4) В любой точке х0 разница Fξ(х0+0) - Fξ(х0) равна P(ξ = х0):

Следствие 3. Если функция распределения Fξ(x) непрерывна в точке х0, то

P(ξ = х0) = 0

F5) Для любой случайной величины ξ имеет место равенство P(а £ ξ < b) = Fξ(a) - Fξ(b).

Если же функция распределения Fξ(x) непрерывна (для любого x, или только в точках a и b), то

P(а £ ξ < b) = P(а < ξ < b) = P(а £ ξ £ b) = P(а < ξ £ b) = Fξ(a) - Fξ(b)

Функция распределения дискретного распределения

Мы уже видели, как выглядят функции распределения некоторых дискретных распределений. Из свойств (F4), (F5) следует

Свойство 4. Случайная величина ξ имеет дискретное распределение тогда и только тогда, когда функция распределения Fξ — ступенчатая функция. При этом возможные значения ξ — точки ai скачков Fξ, и

pi = P(ξ = ai ) = Fξ (ai + 0) - Fξ (ai )— величины скачков.

В следующей главе мы рассмотрим случайные величины, функции распределения которых не удовлетворяют свойству 4 хотя бы потому, что они вовсе не имеют разрывов. Более того, мы выделим класс функций распределения, которые «восстанавливаются по своей производной» с помощью интегрирования (так называемые абсолютно непрерывные функции).

Раздел 8. Абсолютно непрерывные распределения

Определение 28.Случайная величина ξ имеет называемые абсолютно непрерывное распределение, если существует неотрицательная функция fξ(x) такая, что для любого х Î R функция распределения Fξ(x) представима в виде

При этом функция fξ(x) называется плотностью распределения случайной величины ξ.

Теорема 21.Плотность распределения обладает свойствами:

(f1) fξ(x)³ 0 для любого x;

(f2)

Эти два свойства полностью характеризуют класс плотностей:

Лемма 2. Если функция f обладает свойствами (f1) и (f2), то существует вероятностное пространство и случайная величина ξ на нем, для которой f является плотностью распределения.

Доказательство. Пусть Ω есть область, заключенная между осью абсцисс и графиком функции f (« подграфик» функции f). Площадь области Ω равна 1 по свойству (f2). И пусть случайная величина ξ есть абсцисса точки, наудачу брошенной в эту область.

Тогда (вспомнить геометрическую вероятность) для любого х Î R

Свойства плотностей

(f3) Если случайная величина ξ имеет абсолютно непрерывное распределение, то ее функция распределения всюду непрерывна.

Следствие 4. Если случайная величина ξ имеет абсолютно непрерывное распределение, то P(ξ = х) = 0 для любого х Î R.

(f4) Если случайная величина ξ имеет абсолютно непрерывное распределение, то ее функция распределения дифференцируема почти всюду, и

для почти всех х.

Замечание 12. Термин для «почти всех» означает «для всех, кроме (возможно) х из некоторого множества нулевой меры (длины)». Заметьте, что стоящую под интегралом функцию можно изменить в одной точке (или на множестве нулевой длины), и интеграл (« площадь подграфика») от этого не изменится.

(f5) Если случайная величина ξ имеет абсолютно непрерывное распределение, то

Доказательство. Действительно,

Остальные равенства вытекают из следствия 5.

8.1 Примеры абсолютно непрерывных распределений

Равномерное.

Это распределение нам уже знакомо. Говорят, что ξ имеет равномерное распределение на отрезке [a, b], и пишут ξ Î Ua,b если

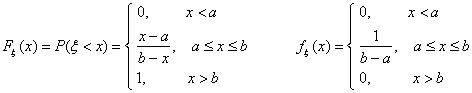
Заметьте, что в точках a и b функция распределения недифференцируема, и плотность можно задать как угодно.

Показательное.

Говорят, что ξ имеет показательное распределение с параметром α, α > 0 и ξ Î Еα, если

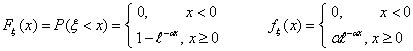
Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство «не старения» (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).

Теорема 21. Свойство «Не старения». Пусть ξ Î Еα. Тогда для любых х, у > 0

Нормальное.

Говорят, что ξ имеет нормальное распределение с параметрами а и σ2 , где а Î R, σ > 0, и пишут ξ Î если ξ имеет следующую плотность распределения:

для любого x Î R

Убедимся, что fξ(x)действительно является плотностью распределения. Так как fξ(x) > 0 для всех x Î R, то свойство (f1) выполнено. Проверим выполнение (f2). Используем табличный интеграл (интеграл Пуассона)

Нормальное (иначе называемое гауссовским по имени Карла Гаусса распределение играет исключительно важную роль в теории вероятностей, поэтому мы очень подробно изучим все свойства этого распределения.

8.2 Свойства нормального распределения

Нормальное распределение задается, как мы видим, с помощью плотности распределения. Связано это с тем, что нельзя выписать первообразную от функции иначе как в виде интеграла, поэтому функцию распределения этого закона можно записать лишь в таком виде: