Биномиальное распределение.

Говорят, что случайная величина ξ имеет биномиальное распределение с параметрами n и p, где 0 £ p £, n и пишут ξ Î Вn,р, если ξ принимает значения 0, 1, …,n с вероятностями P(ξ = k) = Cnk pk (1-p)n-k . Случайная величина ξ с таким распределением имеет смысл числа успехов в n испытаниях схемы Бернулли с вероятностью успеха р .

Таблица распределения ξ имеет вид

Геометрическое распределение.

Говорят, что случайная величина τ имеет геометрическое распределение с параметром р, где 0 £ p £, n, и пишут τ Î Gр, если τ принимает значения 1, 2, 3, …с вероятностями P(τ = k) = p (1-p)k-1. Случайная величина τ с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха р .

Таблица распределения τ имеет вид

Распределение Пуассона.

Говорят, что случайная величина ξ имеет распределение Пуассона с параметром λ, где λ > 0 , и ξ Î П λ, если ξ принимает значения 0, 1, 2 … с вероятностями

Таблица распределения ξ имеет вид

Гипергеометрическое распределение.

Говорят, что случайная величина ξ имеет гипергеометрическое распределение с параметрами n, N и K, K £ N, n £ N если ξ принимает целые значения от max (0, N - K – n ) до min (K ,n ) с вероятностями

. Случайная величина ξ с таким распределением имеет смысл числа белых шаров среди n шаров выбранных наудачу и без возвращения из урны, содержащей К белых шаров и N-K не белых.

Заметьте, что со всеми этими распределениями мы уже хорошо знакомы.

Но распределения случайных величин далеко не исчерпываются дискретными распределениями. Так, например, если точка бросается наудачу на отрезок [0,1], то можно задать случайную величину, равную координате этой точки. Но число значений этой случайной величины несчетно, так что ее распределение дискретным не является. Да и вероятность этой случайной величине принять каждое из своих возможных значений (попасть в точку) равна нулю. Так что не только таблица распределения не существует, но и соответствие «значение величины « вероятность его принять» ничего не говорит о распределении случайной величины.

Какими же характеристиками еще можно описать распределение?

Раздел 7. Функция распределения

Заметим, что на том же отрезке [0, 1] вероятности попадания в множества положительной меры совсем не нулевые. И термин «наудачу» мы когда-то описывали как раз в терминах вероятностей попадания в множество. Может быть, разумно описать распределение случайной величины, задав для любого множества, вероятность принять значения из этого множества? Это действительно полное описание распределения, но уж очень трудно с ней работать — слишком много множеств на прямой.

Нельзя ли обойтись заданием вероятностей попадания в какой-нибудь меньший набор множеств на прямой? Оказывается, что можно ограничиться только вероятностями попадания в интервалы (-¥, х) для всех х Î R, с помощью которых можно будет определить и вероятность попасть в любое другое множество.

Замечание 11. Можно с таким же успехом ограничиться набором вероятностей попадания в интервалы (-¥, х], или в (х ,¥), или в [х ,¥), или в (х1 ,x2). Впрочем, последних уже слишком много.

Определение 27.Функцией распределения случайной величины ξ называется функция Fξ(x) : R ® [0, 1], при каждом x Î R равная Fξ(x) = P(ξ < x) = P{ω: ξ(ω) < x}

Пример 22. Случайная величина ξ имеет вырожденное распределение Ic. Тогда

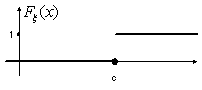
Пример 23. Случайная величина ξ имеет распределение Бернулли Вр. Тогда

Пример 24. Будем говорить, что случайная величина ξ имеет равномерное распределение на отрезке [a, b] и писать ξ Î Ua,b (“ uniform”), если ξ — координата точки, брошенной наудачу на отрезок [a, b] числовой прямой. Это распределение можно задать и с помощью функции распределения:

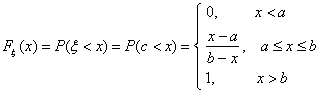
7.1 Свойства функции распределения

Теорема 19.

Функция распределения Fξ(x) обладает следующими свойствами:

F1) Функция распределения Fξ(x) не убывает: если х1 < x2 то Fξ(x1)< Fξ(x2);

F2) Существуют пределы

и