а тогда

.

Пусть . Для построения искомой функции положим

, , .

Функции , , имеют равномерно ограниченную по r вариацию на :

.

Следовательно, по теореме Хелли [2] найдутся функция ограниченной вариации и последовательность , такие, что в каждой точке и

(32)

для любой функции . При этом для n=1,2, .

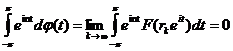
(мы учли аналитичность функции F(z) в единичном круге) и , следовательно, по теореме 3 абсолютно непрерывна : существует функция , для которой

,

Тогда

, (33)

Зафиксируем число . Функция , аналитична в круге , поэтому согласно утверждению 1

, .

В пределе при из последнего равенства вытекает, что

, , .

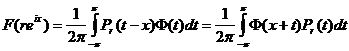Равенство 1) , а вместе с ним и теорема 4 доказаны.

§I.3.Пространства и .

Обозначим через класс тех функций , , которые являются граничными значениями функций из , т.е. представимы в виде

для п.в. , .

В силу пунктов 3) и 2) теоремы 4 и каждая функция удовлетворяет условию (16). С другой стороны, выше мы доказали, что для произвольной с условием (16) интеграл Пуассона (17) определяет функцию из . Следовательно,

. (34)

Из (34) вытекает, что (замкнутое) - подпространство пространства , а - банахово пространство с нормой (15).

Пусть . Положим

,

, (35)

ОпределениеI.5.

Если функция , то сопряженной к ней функцией называется функция , ,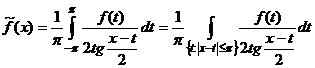

где интеграл понимается в смысле главного значения, т.е. как предел при интегралов .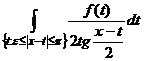

В дальнейшем нам понадобится

Утверждение2.

Для любой функции сопряженная функция существует и конечна п.в. на ; при этом

а) , y>0;

б) если , , то и .

Теорема 5.

Следующие условия эквивалентны :

а) ;

б) , , , ;

в) ;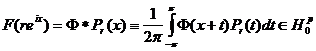

г) , где - такая действительная функция, что ее сопряженная также принадлежит пространству :