Содержание

Введение 3

Глава I. Основные сведения об интеграле Пуассона и

пространствах , и . 8

§I.1. Интеграл Пуассона . 8

§I.2. Пространства . 12

§I.3. Пространства и . 17

§I.4. Произведение Бляшке, нетангенциальная

максимальная функция . 22

Глава II. Атомические разложения функции в пространстве

, пространство ВМО 26

§II.1. Пространство , критерий принадлежности

функции из пространству . 26

§II.2. Линейные ограниченные функционалы на ,

двойственность и ВМО 32

Литература 37

Введение.

Целью настоящей работы является изучение основных понятий и результатов, полученных в области пространств Харди, которая не изучалась в рамках университетского курса. В работе прослежена взаимосвязь между следующими понятиями : интеграл Пуассона, пространства , , и , раскрыта суть и структура этих объектов. Описание указанных понятий вводится именно в такой последовательности , так как определение каждого последующего объекта дается на основе понятий, расположенных левее в выше перечисленном ряду объектов.

Работа состоит из двух глав, каждая из которых делится на параграфы. В первой главе изучены свойства пространств , , , а во второй мы доказываем коитерий принадлежности функции из пространству и двойственность пространств и .

В работе мы рассматриваем случай периодических функций. Используемые обозначения имеют следующий смысл:

- пространство периодических, непрерывных на функций;

- пространство периодических, бесконечно дифференцируемых на функций;

- пространство периодических, суммируемых в степени р на функций, т.е.для которых , ;

- пространство периодических ограниченных на функций;

- носитель функции .

В §I.1.вводится понятие интеграла Пуассона: интегралом Пуассона суммируемой на [-p,p] 2p-периодической комплекснозначной функции называется функция

¦r ( x ) = ,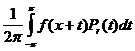

где , t Î [ -p, p ] - ядро Пуассона.

Здесь мы доказываем следующие свойства ядра Пуассона, которые мы неоднократно будем использовать в ряде доказательств:

а) ;

б) ;

в) для любого d>0

Основной целью данного параграфа являются две теоремы о поведении интеграла Пуассона при :

Теорема 1.

Для произвольной (комплекснозначной) функции ( -p, p ) , 1 £ p < ¥ , имеет место равенство

;

если же ¦ (x) непрерывна на [ -p, p ] и ¦ (-p) = ¦ (p) , то

.

Теорема 2 (Фату).

Пусть - комплекснозначная функция из . Тогда

для п.в. .

В этом параграфе мы обращались к следующим понятиям:

Определение1. Функция называется аналитической в точке , если она дифференцируема в этой точке и в некоторой ее окрестности. Говорят, что функция аналитична на некотором множестве,если она аналитична в каждой точке этого множества.

Определение2. Действительная функция двух действительных переменных называется гармонической в области , если и удовлетворяет уравнению Лапласа:

.