¦r ( x ) = 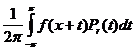, ( 3 )

где

, t Î [ -p, p ] . ( 4 )

Функция двух переменных Рr (t) , 0 £ r <1 , t Î [ -p, p ] , называется ядром Пуассона , а интеграл (3) - интегралом Пуассона .

Следовательно,

Pr ( t ) = , 0 £ r < 1 , t Î [ -p, p] . ( 5 )

Если ¦Î L1 ( -p, p ) - действительная функция , то , учитывая , что

c-n ( f ) = , n = 0, ±1, ±2,¼, из соотношения (2) мы получим :

fr ( x ) =

= , ( 6 )

где

F ( z ) = c0 ( f ) + 2 ( z = reix ) ( 7 )

- аналитическая в единичном круге функция как сумма равномерно сходящегося по х ряда [5]. Равенство (6) показывает, что для любой действительной функции ¦Î L1( -p, p ) интегралом Пуассона (3) определяется гармоническая в единичном круге функция

u ( z ) = ¦r (eix ) , z = reix , 0 £ r <1 , x Î [ -p, p ] .

При этом гармонически сопряженная с u (z) функция v (z) c v (0) = 0 задается формулой

v (z) = Im F (z) = . ( 8 )

Утверждение1.

Пусть u (z) - гармоническая ( или аналитическая ) в круге | z | < 1+e ( e>0 ) функция и ¦ (x) = u (eix) , xÎ[ -p, p ] . Тогда

u (z) = ( z = reix , | z | < 1 ) ( 10 )

Так как ядро Пуассона Pr (t) - действительная функция, то равенство (10) достаточно проверить в случае, когда u (z) - аналитическая функция:

=, | z | < 1+ e .

Но тогда коэффициенты Фурье функции связаны с коэффициентами Фурье функции следующим образом :

и равенство (10) сразу следует из (2) и (3).

Прежде чем перейти к изучению поведения функции ¦r (x) при r®1 , отметим некоторые свойства ядра Пуассона:

а) ;

б) ; (11)

в) для любого d>0

Соотношения а) и в) сразу следуют из формулы (5), а для доказательства б) достаточно положить в (2) и (3) ¦ (х) º 1.

Теорема 1.

Для произвольной (комплекснозначной) функции ( -p, p ) , 1 £ p < ¥ , имеет место равенство

;

если же ¦ (x) непрерывна на [ -p, p ] и ¦ (-p) = ¦ (p) , то

.

Доказательство.

В силу (3) и свойства б) ядра Пуассона

. ( 12 )

Для любой функции , пользуясь неравенством Гельдера и положительностью ядра Пуассона , находим

.

Следовательно,

.

Для данного e > 0 найдем d = d (e) такое, что . Тогда для r , достаточно близких к единице, из свойств а)-в) мы получим оценку

.

Аналогично, второе утверждение теоремы 1 вытекает из неравенства

.

Теорема 1 доказана.

Дадим определения понятий "максимальная функция" и "оператор слабого типа", которые понадобятся нам в ходе доказательства следующей теоремы.

ОпределениеI.1.

Пусть функция , суммируема на любом интервале (a,b), a<b, . Максимальной функцией для функции называется функция

,

где супремум берется по всем интервалам I , содержащим точку х.

Определение I.2.

Оператор называется оператором слабого типа (р,р) , если для любого y > 0

, .

Теорема 2 (Фату).

Пусть - комплекснозначная функция из . Тогда

для п.в. .

Доказательство.

Покажем, что для и

, ( 13 )

где С - абсолютная константа , а M ( f, x ) - максимальная функция для f (x)*). Для этой цели используем легко выводимую из (5) оценку

(К - абсолютная константа).

Пусть - такое число, что