Всю систему взаимообусловленности истинностных значений суждений с одинаковой материей удобно изобразить графически с помощью так называемого логического квадрата.

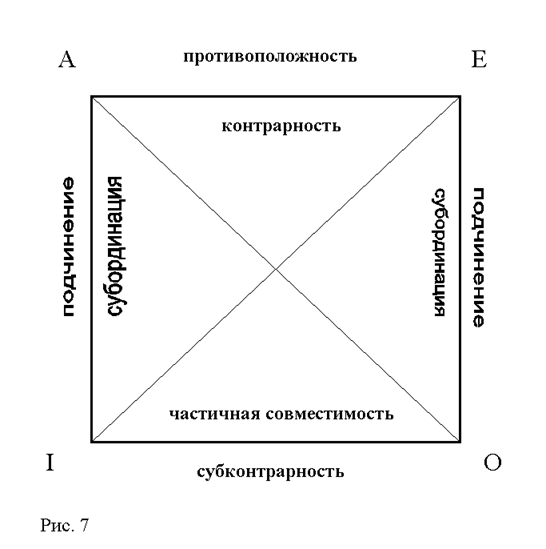
Буквы на его углах символизируют различные виды суждений - A, E, I, O (см. рис. 7). А его стороны и диагонали выражают всю совокупность возможных отношений между ними. Линия AE образует отношение противоположности или, иначе, контрарности. Пары этих суждений никогда не могут быть одновременно истинными; в нашем примере истинность того и другого означала бы, что верно как утверждение о том, что все киоски в этом квартале торгуют цветами, так и о том, что ни один из них ими не торгует. Очевидно, такое невозможно. Другие же сочетания значений для пары S a P и S e P допустимы: могут быть оба ложны, и может одно быть истинным, а другое ложным. Отсюда получается правило: когда одно из противоположных суждений (S a P или S e P) истинно, то можно уверенно делать вывод, что противоположное ему истинным не является, когда же одно ложно, то никаких выводов о противоположном делать нельзя, оно может быть и тем, и другим.

Две расположенные по диагонали пары AO и EI составляют отношение противоречия или контрадикторности. Их истинностные соотношения легче всего запомнить: они не бывают ни одновременно истинными, ни одновременно ложными. Следовательно, их истинностные значения регулируются законом исключенного третьего: когда одно истинно, другое обязательно ложно и наоборот. Это значит, установив истинностное значение одного из членов пары, каким бы оно ни было, мы тем самым однозначно установили значение лежащего против него по диагонали.

Нижняя сторона квадрата IO выражает отношение частичной совместимости, или, иначе, субконтрарности. В отличие от противоположных суждений эта пара никогда не бывает одновременно ложной. В принципе можно рассматривать данное обстоятельство как следствие, обусловленное первыми двумя отношениями. В самом деле, попробуем воспользоваться теми соображениями, которые были высказаны о противоположных и противоречащих суждениях, предположив сначала, что S i P ложно, и определив значение S o P в таком случае, затем проделаем то же самое, отправляясь от того, что ложно S o P. Итак, допустим, что S i P ложно. Тогда противоречащее ему суждение S e P истинно (ибо лежащие по диагонали пары не могут быть вместе ни истинными, ни ложными); отсюда следует, что противоположное S e P суждение S a P должно быть ложным (так как из противоположных пар суждений истинным может быть только одно); но, установив ложность S a P, мы обязаны признать истинным противоречащее ему суждение S o P. Совершенно аналогично, допустив ложность S o P, мы обратным порядком придем к утверждению, что S i P в таком случае должно быть истинно. Однако при других истинностных значениях их взаимообусловленность отсутствует. Предположив, что S i P (S o P) истинно, мы сможем, правда, прийти к выводу о ложности противоречащего ему суждения S e P (S a P), но дальше рассуждение оборвется, так как при ложности одного из противоположных понятий другое может иметь любое из двух возможных значений, а значит и лежащее против него по диагонали противоречащее (и одновременно субконтрарное относительно S i P) суждение S o P может быть как истинным, так и ложным. Таким образом, получается правило в отношении субконтрарных суждений: когда одно из них ложно, другое обязательно истинно, но когда одно из них истинно, то о другом ничего сказать нельзя.

Стороны квадрата AI и EO выражают отношение подчинения или субординации. В какой-то мере его можно было бы уподобить отношению части и целого: истинность общего суждения (и утвердительного S a P, и отрицательного S e P) означает одновременно истинность частного (S i P и соответственно S o P). Если мы знаем, что все металлы электропроводны, то тем более верно говорить это о некоторых из них. Однако когда общее суждение ложно, то о частном сказать ничего нельзя; к примеру, отрицание того, что все представители данной философской школы - идеалисты, может означать как то, что их там только часть, так и то, что их там вообще нет. При движении же от частного к общему все обстоит наоборот. Лишь когда частные суждения ложны, можно делать вывод о том, что подчиняющее его суждение тоже ложно (если неверно, что часть предметов обладает (не обладает) каким-то свойством, то тогда тем более неверно сказать то же самое про все). Но если частное суждение истинно, то это оставляет нас в неведении относительно истинности или ложности общего суждения. Мы можем, например, узнать, что некоторые медведи в данной географической зоне бурые; это обстоятельство, однако, не позволит нам узнать, есть ли там еще и другие медведи или они все там бурые. Итак, основываясь на выводах об истинности общего суждения S a P и S e P, можно прийти к заключению об истинности подчиненных им суждений S i P и соответственно S o P, а от ложности частного суждения S i P и S o P можно прийти к утверждению о ложности соответствующих подчиняющих суждений S a P и S e P. При ложности же общих и истинности частных суждений никакие выводы по линии подчинения невозможны.

И это правило тоже можно получить в качестве следствия из отношений противоречия и противоположности. Так, если общее суждение S a P (S e P) истинно, то тогда обязательно ложно противоположное ему суждение S e P (S a P), а отсюда по линии противоречия получим, что истинно подчиненное по отношению к S a P (S e P) суждение S i P (S o P). И таким же путем, предположив ложность частных суждений, мы придем к выводу о ложности подчиняющих их общих. При других исходных значениях рассуждения не получатся из-за того, что при ложности общих суждений не допускаются выводы по линии противоположности.

Необходимо помнить о том, что теория логического квадрата построена только для неопределенно-частных суждений, когда под словом "некоторые" подразумевается "как минимум некоторые, а может быть и все". На определенно-частные, или выделяющие суждения с квантором "только некоторые", она не распространяется. Система отношений истинностных значений для этого случая не укладывается в квадрат, но зато она выглядит проще. 1) Когда истинно одно из общих суждений, то все остальные обязательно ложны; обратное тоже верно. 2) Частные суждения либо оба вместе истинны (и тогда оба общих ложны), либо оба вместе ложны (и тогда одно из общих истинно, а одно ложно).

Законы логического квадрата, как и остальные логические законы, не зависят от содержания высказываний. О чем бы ни шла речь, все отмеченные правила действуют неукоснительно. Даже если нам непонятно содержание, то все равно, опираясь на одну только логическую форму, можно сделать правильные выводы или проверить, верно или нет построено то или иное рассуждение с использованием суждений одинаковой материи.

Допустим, перед нами такой текст: "Неправильно говорить, что (1) некоторые целлы представляют собой наосы, и еще более ошибочно считать, будто (2) никакие целлы не являются наосами". Чтобы разобраться с содержанием этих мало кому известных понятий, надо сначала решить, каковы эти суждения по качеству и количеству и какое между ними отношение. Первое из них частноутвердительное - S i P, второе - общеотрицательное - S e P. Следовательно, они расположены по диагонали квадрата EI и между ними отношение противоречия (не могут быть вместе как истинными, так и ложными). Высказывание же объявляет их оба ложными. Отсюда мы можем заключить, что первое суждение может быть только определенно-частным и означает: "Только некоторые целлы есть наосы", которое объявляется ложным вместе с общеотрицательным суждением (2). Из истинностных соотношений для суждений с таким квантором следует, что частные суждения бывают ложными лишь одновременно. Тогда значит и суждение частноотрицательное тоже надо признать ложным. Истинным остается только общеутвердительное суждение S a P: "Все целлы - наосы" (то и другое представляет собой название главного помещения в древнегреческом храме, то есть эти слова синонимы).