l=1

В данном случае согласно правил квантования уже три проекции.

Следовательно на р-подуровне три р-орбитали. рис2.2.

Для d-подуровня: l=2, ml = –2, –1, 0, +1, +2. Это значит, что согласно квантовой теории d-подуровень состоит из пяти d-орбиталей.

Подуровень f имеет l=3, ml = –3, –2, –1, 0, +1, +2, +3. Следовательно f-подуровень состоит из семи f-орбиталей.

Число орбиталей на подуровне можно определить из выражения ml =2l+1:

значение l: 0, 1, 2, 3, …….

подуровень: s, p, d, f, …….

число орбиталей: 1, 3, 5, 7, …….

Спиновое квантовое число ms характеризует собственный момент количества движения, возникающий как бы из-за «вращения» электрона вокруг собственной оси. Принимает два значения: +1/2 и –1/2, что соответствует двум возможным направлениям вращения электрона.

ms= +1/2; –1/2.

Оно получено из опытов Штерна и Герлаха.

Рассмотренные квантовые числа определяют энергию электрона, объем и форму пространства, в котором вероятно его пребывание в околоядерном объеме, т.е. размер, форму и ориентацию орбитали в пространстве.

Так как волновая функция y является решением уравнения Шредингера при всевозможных значениях квантовых чисел, то можно сказать, что волновая функция является в свою очередь функцией рассмотренных квантовых параметров n, l и ml, где:

n= 1, 2, 3, 4,…,

l= 0, 1, 2, 3,…,n–1

ml=–l,…, –1, 0, +1,…, +l

Атомные орбитали. Так как вероятность нахождения электрона в пространстве далеком от ядра очень мала, когда говорят об орбиталях, то имеют в виду такую область вокруг ядра атома внутри которой сосредоточено 90–95% электронного заряда. С точки зрения квантовой механики атомные орбитали являются геометрическим изображением волновой функции y (n, l, ml).

Z Электронное облако. Если бы в каждый момент времени

y определяли положение электрона в трехмерном пространстве и

ставили в том месте точку, то через множество таких определений

X получили бы картину в виде пространственного облака изображен-

ного точками с размытыми краями /рис.2.3.)

рис.2.3.

Такое зарядовое облако называют электронным облаком. Его плотность, пропорциональная y2, является непосредственной мерой вероятности нахождения электрона. Граничная поверхность облака, внутри которой содержится 90–95% электронного заряда, дает форму орбитали.

Z s-орбиталь. Она существует при l=0. Значение ml тоже равно

Y нулю. Имеем только одно значение ml =0. Следовательно,

s-орбиталь имеет максимальную симметричность. У нее

X сферическая форма (рис.2.4.). В этом случае вероятность на–

хождения электрона в околоядерном пространстве определя–

рис.2.4. ется только радиусом-вектором и не зависит от угла координат.

y Радиальное распределение электронной плотности для 1s

электрона соответствует кривой с максимумом (рис.2.5.).

Максимум распространения вероятности находится на

0 r1 r,A0 расстоянии от ядра r1, которые соответствует радиусу

рис.2.5. первой боровской орбиты.

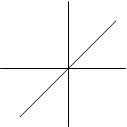
р-орбиталь. Существует при l=1. ml = –1, 0, +1.

Z р-орбиталь появляется на втором и всех последующих

Рz уровнях. Так как ml имеет три значения, то на р-подуров-

Y не каждого уровне может быть три р-орбитали. р-орбиталь

имеет гонтелеобразную форму. Все три р-орбитали распо-

X лагаются в пространстве по направлению координатных

Px осей. Их называют соответственно рх, рy, рz-орбитали

Py (рис.2.6.).

Рис.2.6. Z Y Y Z Z

X X X X Y

dz2 dx2 y2 dxy dxz dyz

рис.2.7.

d-орбиталь. Появляется при l=2 на третьем квантовом уровне. На d-подуровне может быть уже пять различных состояний электронов, поэтому на d-подуровне каждого квантового уровня содержится пять d-орбиталей. В этом случае ml принимает пять значений: ml = –2, –1, 0, +1, +2, d-орбитали имеют более сложную форму, чем р-орбитали, они либо в виде четырех лепестков либо в виде гантели с ободком (рис.2.7.).

f-орбиталь. Появляется при значении l=3. f-орбитали могут быть только на четвертом и более отдаленных уровнях. Так как при l=3 ml имеет 7 значений /–3, –2, –1, 0, +1, +2, +3/, то на f-подуровне может быть семь орбиталей. Форма f-орбиталей еще более сложная, чем у d-орбиталей. f-орбитали изображают в виде сложных шестилепестковых фигур.

Форма орбиталей и ее направленность играют существенную роль при образовании химических связей, т.к. эти два фактора определяют характер и степень перекрывания электронных облаков соединяющихся атомов.

2.1.5. Структура электронных оболочек атомов.

Полная электронно-энергитическая структура атомов предопределяется набором рассмотренных квантовых чисел. Главное квантовое число n определяет не только номер квантового уровня, но и указывает на число подуровней содержащихся в данном уровне. Например, при n=3, имеем третий квантовый уровень, который состоит из трех подуровней: s-, p-, d-подуровня. Чем дальше от ядра находится квантовый уровень, тем он более емкий, тем из большего числа подуровней он состоит. Число орбиталей на уровне можно определять по формуле кn=n2, а число орбиталей на подуровне, как уже указывалось, по формуле кl=2l+1.

Рассмотрим теоретическую схему взаимного расположения квантовых уровней и подуровней. /Фрагмент для первых четырех уровней/. На четырех вертикальных линиях отложим значения квантовых чисел n, l, ml и ms.(рис.2.8.) На первой вертикальной линии изобразим квантовые уровни соответственно значениям квантового числа n /см. рис.2.8.). Мы уже знаем, что чем больше числовое значение n, тем более емкий квантовый уровень. По этому на рисунке он сделан более длинным по высоте. На второй вертикальной линии, отнесенной к квантовому числу l показано деление квантовых уровней на подуровни. Первый квантовый уровень состоит только из одного подуровня /обозначенного как s-подуровень/. Второй квантовый уровень делится уже на два подуровня: s-подуровень и р-подуровень. Третий уровень делится на три подуровня /s, p и d/, а четвертый – на четыре подуровня /s, p, d и f/.