åx = 15; åy = 32; åx2 = 55; åxy =112.

Обозначения здесь такие же, что и в предыдущем примере. Бук­вы заменяются их числовыми значениями.

5a + 15b = 32;

15a + 55b = 112.

Члены первого уравнения умножаются на 3

15a + 45b = 96.

Из второго уравнения вычитается первое, получим значение b:

10b= 16; b= 1,6.

Из первого уравнения получаем значение а:

5a + 24 = 32;

5a = 8; a = 1,6.

Можно получить сглаженные показатели по дням упражнений у Толи. y1 = 1,6 + 1,6=3,2;

y2 = 1,6+3,2=4,8;

y3 = 1,6 + 4,8 = 6,4;

y4 = 1,6 + 6,4 = 8,0;

y5 = 1,6+ 8,0=9,6.

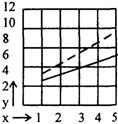
На рис. 6 показаны только результаты сглаживания. Следует обратить внимание на то, как различаются отрезки прямой по их наклону по отношению к оси абсцисс. Дан­ные Толи изображены пунктирной прямой.

Таковы способы обработки задач третьего типа.

Задачи, встающие перед психологом, который работает в области психологи­ческой диагностики, составляют четвер­тый тип задач.

Они относятся к конструированию диагностических методик, к их применению и обработке. Американская психологическая ассоциация (АПА) периодически издает «Стандартные требования к педагогическим и психологическим тестам», специальный кодекс требований к диагностическим методикам; это пособие полезно как для авторов методик, так и для тех, кто методиками пользуется.

Некоторые из этих требований могут считаться дискуссионными, но полезность кодекса в целом несомненна. Его выполнение, с одной сто­роны, обеспечивает объективность методик и их обоснованность, а с другой — препятствует проникновению в арсенал методик психологи­ческой диагностики дилетантских поделок, произвольных наборов все­возможных заданий, заимствованных из популярных журналов или со­чиненных самим автором. Самые общие и самые необходимые к испол­нению требования можно было бы свести всего к двум: диагностиче­ские методики должны быть надежными и валидными. Значение этих терминов было дано в предыдущих главах. Реализация этих требований осуществляется посредством прочно вошедших в психологическую ди­агностику статистических методов (Как было показано в гл. XI, при работе с критериально-ориентированными методиками при их конструировании и проверке возможны другие подходы).

Чтобы получить коэффициент надежности, характеризующий го­могенность методики, ее внутреннюю согласованность, прибегают к приему, называемому расщеплением. Эксперимент проводится с вы­боркой желательно порядка 100, но не менее 50 испытуемых. Полу­ченные от каждого участника выборки ответы на вопросы или ре­шения заданий делятся на четные и нечетные — по их нумерации в методике. По каждой половинке методики выписывается число пра­вильно выполненных каждым испытуемым заданий. Два эти ряда коррелируют между собой.

Допустим, что методика состоит из 24 заданий. Тогда максимальное число выполненных заданий в каждой половинке будет равно 12. Приводим результаты первых 16 испытуемых и технику вычисления коэффициента надежности (гомогенности) r (табл. 8).

Таблица 8

ВЫЧИСЛЕНИЕ КОЭФФИЦИЕНТА НАДЕЖНОСТИ МЕТОДИКИ А (ГОМОГЕННОСТЬ)