В моделях, основанных на представлении об адаптационном ресурсе принцип Либиха допускает такую формулировку: при данном распределении ресурса в случайно выбранных условиях коэффициент размножения будет, как правило, функцией преимущественно одного фактора (или небольшого их числа). Простейшая модель формализации строится так. Рассматривается средний коэффициент размножения (при фиксированном распределении ресурса) в непрерывном времени, т.е. коэффициент в уравнении (- численность популяции). Предполагается, что допускает разбиение в сумму , где 0 не зависит от численности , а 1 - функция , не зависящая от распределения ресурса. Давление каждого фактора характеризуется числом , на борьбу с i- м фактором мобилизуется ресурс , нормировка выбрана так, что значение =0 отвечает оптимуму, распределение ресурса ri удовлетворяет ограничению . Реальное воздействие i- го фактора на выживание и смертность характеризуется числом . Согласно принципу Либиха, коэффициент0 определяется тем фактором, для которого максимально:

k0=j((fi - ri)), (1)

где j - некоторая монотонно убывающая функция.

Возникает вопрос о выборе распределения ресурса ri. Он решается с помощью принципа оптимальности Холдейна [10,33,37]: параметры особи, складывающиеся в ходе эволюции (сукцессии, адаптации), должны доставлять минимум коэффициенту размножения. Для зависимости (1) это означает, что максимальное значение fi - ri должно быть минимальным из возможных, т.е. распределение должно быть решением задачи:

,

, . (2)

Если , то решение (2) будет ri=fi. В противном случае 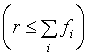ее решение дается выражениями:

,

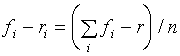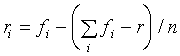, (3)

где n - количество факторов.

Согласно (3), разность fi - ri одинакова для всех факторов, и отклонение любого фактора от установившегося значения окажет влияние на коэффициент размножения k0 (1).

Итак, от простейшей формализации принципа Либиха (!) с помощью зкстремального принципа Холдейна приходим к принципу полифакториальности: в результате эволюции (сукцессии, адаптации) устанавливается такое распределение ресурса, которое делает все факторы равнозначными.

Здесь возникают два вопроса: во-первых, насколько полученный вывод зависит от вида модели (1) и, во-вторых, насколько правомерно использовать один и тот же принцип Холдейна для описания принципиально различных процессов: эволюции, сукцессии, адаптации.

Модель (1) является простейшей формализацией принципа Либиха. Ее небольшие вариации не меняют сути дела. Так, если

k0 = j((ai fi - biri)), (ai, bi>0), (4)

то вместо задачи (2) получаем

(5)

Ее решение дается аналогом (3): если

то ri=aifi/bi,

в противном случае

ri=(aifi-r)/bi, (6)

где

r.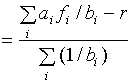

И все aifi-biri равны r: максимум в (4) достигается сразу при всех i. Отклонение давления каждого фактора от fi (превышение при данном распределении ресурса) оказывает влияние на коэффициент размножения.

Следующее обобщение (1), сохраняющее принцип Либиха (коэффициент размножения определяется тем фактором, который находится далее всего от оптимума), дается зависимостью

k0 = j0 (Фi(jI(bifi) - yi(ri)) (7)

где j0 - монотонно убывающая, а Фi, ji, yi (i³1) - монотонно возрастающие функции. Здесь «степень отклонения от оптимума» измеряется величиной Фi(ji(fi)-yi(ri)). Дополнительное условие: Фi(0)= ji(0)= yi(0)=0 (нормировка). И для модели (7) максимум коэффициента размножения достигается в тех случаях, когда все значения Фi(ji(fi)-yi(ri)) равны между собой. Для доказательства достаточно заметить, что если для некоторого i=i0

(8)

то можно уменьшить ri на некоторое достаточно малое , увеличив при этом те ri, для которых в (8) достигается максимум на /m (m - число таких ri), так, что значение максимума, а следовательно, и k0 (7) уменьшатся.

Закончим данный раздел изложением еачественных соображений. Если верен принцип Либиха, и в случайно выбранных условиях выживание и (или) размножение лимитируется одним фактором или небольшим их числом, то сложившаяся в ходе эволюции система распределения адаптационного ресурса должна быть устроена таким образом, чтобы перераспределять ресурсы на борьбу с этими лимитирующими факторами, на компенссцию лимитирования и тем самым должна вести к полифакториальности.

4. Использование принципа Холдейна для описания адаптации

Экстремальный принцип Холдейна был выдвинут для описания процесса эволюции [33, 37]. Для его использования следует зафиксировать множество, на котором идет отбор, и исследовать точки экстремума среднего коэффициента размножения на этом множестве. Существуют теоремы об эффективности отбора [8, 33], согласно которым со временем в ходе отбора остается сравнительно небольшая часть исходного разнообразия, соответствующая указанным точкам экстремума. Принцип максимального среднего коэффициента размножения и называется принципом Холдейна.