В это время болельщикам предлагают задание доказать теорему. Три человека от каждой команды доказывают теорему письменно. Теоремы написаны на листах, болельщики их выбирают и доказывают.

После истечения времени болельщики сдают листки на проверку в жюри и садятся на свои места.

Слово дают команде, которая уже справилась с заданием, она читает вопрос и отвечает на него, то есть показывает свой чертеж. После этого слово передается другой команде.

Гейм 4. «Дальше, дальше, дальше…» (10 минут).

Ведущий: Это наш последний гейм. В этом гейме мы узнаем какая же команда была сильнее. Поэтому, чтобы не терять времени давайте приступим к нему. Каждой команде за 3 минуты необходимо быстро ответить на 20 вопросов. Если за 3 минуты отведенного времени все ответы правильные, команда получает 10 премиальных очков. В этом гейме главное быть быстрым, четким и остроумным и тогда у вас все получиться.

Слово предоставляется команде, у которой пока меньше очков. Затем отвечает на вопросы другая команда.

После этого гейма подводятся итоги.

В то время, когда жюри подводят итоги игроки делятся мнением друг с другом о ходе игры. Учитель слушает и вносит поправки в разработку своей игры.

Примечание: задание для геймов сделаны на отдельных карточках (смотри приложение).

Заключение.

Моя курсовая работа посвящена развитию познавательного интереса к математике, посредством применения игрового момента как на уроках, так и внеурочное время. В курсовой работе рассматриваются как вопросы теории, таки практическая сторона, представленная внеклассным мероприятием: «Веселый математический поезд» и уроком-игрой: « Счастливый случай». В ходе игры все дети были активны, им было интересно, всем хотелось участвовать в игре, показать свои знания и умения быстро реагировать в конкретных ситуациях. Дети внимательно слушали задания и пытались сделать его, как можно лучше. В процессе игры учащиеся показали накопленные знания, умение ориентироваться в математических терминах, а также вспомнили изученные математические понятия.

Игра имеет познавательное значение, расширяется кругозор учеников, способствует развитию памяти, логического мышления. Все поставленные цели были реализованы в процессе проведения внеклассного мероприятия. Но ведь математические игры и развлечения могут быть использованы и во время урока.

Систематическое использование математических игр на разных этапах изучения различного по характеру математического материала является эффективным средством активизации учебной деятельности школьников, положительно влияющим на повышение качества знаний, умений и навы­ков учащихся, развитие умственной деятельности. Словом, математические игры заслуживают право дополнить традиционные формы обучения и вос­питания школьников.

На основе всего вышесказанного можно с уверенностью сказать, что игровые моменты должны внедрятся в учебный процесс и широко использоваться в школе.

Приложение

Счастливый случай.

Гейм 1: «Гонка за лидером».

1-я категория вопросов «четырехугольник».

1. Верно ли, что если диагонали четырехугольника перпендикулярны, то это ромб? Почему?

2. Верно ли, что если в четырехугольнике противоположные углы прямые, то это прямоугольник? Почему?

3. Существует ли четырехугольник с 3 тупыми углами? Доказать?

4. Существует ли такой параллелограмм, который диагональю разбивается на два равносторонних треугольника?

5. Какие одинаковые свойства у прямоугольника и квадрата.

6. Может ли больший угол четырехугольника быть острым? Доказать.

7. Могут ли углы треугольника соответственно равняться трем углам параллелограмма? почему?

8. Швея убеждается в том, что кусок материи имеет форму квадрата: сгибая по каждой его диагонали. Если в обоих случаях края материи совпадают, то она считает, что кусок материи имеет форму квадрата. Правильно ли это или нет?

2-я категория вопросов «площади многоугольников».

1. Параллелограмм и прямоугольник имеют одинаковые стороны. Найти острый угол параллелограмма, если его прямоугольника.

2. Диагональ квадрата равна а. Чему равны его площадь?

3. Параллелограмм и прямоугольник имеют равные основания и равные периметры. Площадь какой фигуры больше и почему?

4. Как надо изменить сторону квадрата, если S его изменить в 4 раза?

5. В трапеции проведены диагонали. Найти 3 пары равновеликих треугольников. Доказать.

6. Что больше: S квадрата а или равностороннего треугольника со стороной а? Почему?

7. Можно ли, зная длины смежных сторон параллелограмма и длину одной из его диагоналей, найти его S? Если да, то как?

8. Правда ли, что, зная катеты прямоугольного треугольника, можно найти высоту, проведенную к гипотенузе? Если да, то как?

Гейм 2 « Спешите видеть».

1)

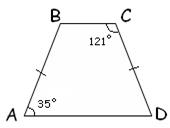
2)

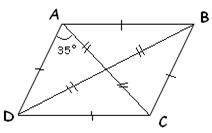
3)

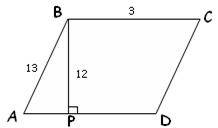
4)

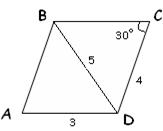
5)

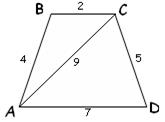
6)

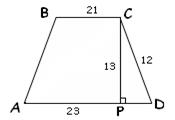
Гейм 3: « Семь раз отмерь – один отрежь».

1. Разрезать трапецию по одной линии так, чтобы из получившихся частей можно было составить треугольник.

2. Треугольник разрезать на 2 треугольника так, чтобы площадь одного из них была вдвое больше площади другого.

3. Разрезать параллелограмм на 3 треугольника так, чтобы площадь одного из них была равна сумме площадей двух других.

4. Разрезать трапецию на 2 равновеликие трапеции.

5. Разрезать параллелограмм по одной линии так, чтобы из получившихся частей можно было составить прямоугольник.

6. Отрезать от параллелограмма треугольник, площадь которого в 4 раза меньше площади данного параллелограмма.

Гейм 4: «Дальше, дальше, дальше…»

1-я команда.

1. Равны ли диагонали прямоугольника?

2. Верно ли, что в параллелограмме сумма противоположных углов ?

3. Формула площади прямоугольника?

4. В каком ромбе сторона равна его высоте?

5. Сколько вершин у четырехугольника?

6. Верно ли, что прямоугольник – это параллелограмм, у которого один угол прямой?

7. Формула площади ромба.

8. Какая трапеция называется равнобедренной?

9. Может ли высота трапеции быть ее диагональю?

10. Формула площади равностороннего треугольника со стороной а?

11. Существует ли параллелограмм, у которого диагонали перпендикулярны?

12. Сколько диагоналей можно провести в треугольнике?

13. Можно ли утверждать, что если в четырехугольнике две противоположные стороны равны, то это параллелограмм?

14. Сколько пар равных сторон у прямоугольника?

15. Может ли квадрат иметь диагонали разной длины.