Начиная с цифры 1 в верхнем левом углу, проведите ломаную линию в нижний правый угол с цифрой 9. При этом двигаться от цифры к цифре можно только либо вправо, либо вниз; сумма цифр, перечеркнутых ломаной, должна равняться 100.

Найдите маршруты, содержащие наименьшее и наибольшее количество «поворотов».

б) Домино.

28 костяных прямоугольных пластинок на которые нанесены очки, составляют домино. На половинках этих косточек представлены все возможные комбинации чисел от 0 до 6. Обычный набор домино – это, как правило, прямоугольные плитки из черной пластмассы с белыми крапинами в виде точек.

Комплект домино – все 28 косточек – идеальный материал для составления комбинационных задач. Может показаться, что 28 костей домино – это не вполне удобное количество, чтобы можно было придумать что-нибудь подходящее. Однако это не так: кости домино, выстроившись в виде квадратов, рамок, пирамид, узоров и так далее, представляют во всем своем многообразии: причудливые формы и богатство содержания настолько очаровывают, что при этим можно часами, не отрываясь, возиться с той или иной головоломкой.

Домино «Дроби»:

Возьмите комплект домино и отложите в сторону кость 0:0. Теперь, рассматривая оставшиеся косточки как дроби (правильные и неправильные), расположите их как на рисунке, чтобы в каждой строке равнялась числу косточек данной строки.

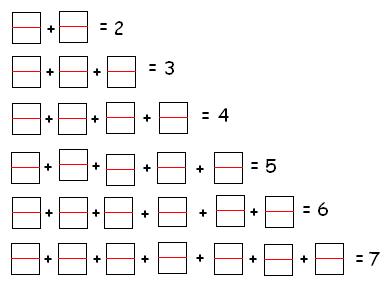
Магическое домино:

Из 28 костей домино сложите прямоугольник 7×8 такой, что если не учитывать семь пустых квадратов, образующих последний столбец, то из 49 клеток будет составлен магический квадрат – «это расположение n2 чисел в n рядов и n колонок таким образом, чтобы суммы чисел в каждом ряду (горизонтали), в каждой колонке (вертикали) и в диагоналях были равны» (в котором суммируются очки половинок костей), суммы очков по горизонтали, вертикали и двум диагоналям которого равны 24.

Коврик из домино:

Уложите все 28 косточек домино в виде коврика так, чтобы сумма очков вдоль каждой прямой (без разрывов) была равна 25. Косточки не обязательно прикладывать друг к другу одинаковыми значениями очков.

Раз спичка, два спичка …

Задачи и головоломки данного раздела могут оказаться к месту и в дальней дороге, и в домашней обстановке, когда накопилась усталость от физического труда или хочется занять свободное время чем-то не очень сложным, дать небольшую работу голове.

Практически всегда под рукой найдется коробочек спичек или коробочек со счетными палочками, с помощью которых легко выложить на столе предлагаемые фигурки и поупражняться с ними.

Это занятие, увлекательное, вольно или невольно способствует развитию терпения, сообразительности, наблюдательности, умения мыслить логически.

Пятнадцать спичек:

Как показано на рисунке, из пятнадцати спичек сложены 5 квадратов.

а) Отнимите 2 спички, чтобы осталось 4 таких же квадрата.

б) Отнимите 3 спички, чтобы осталось 3 квадрата.

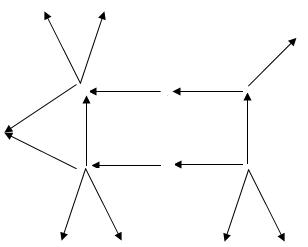
Корова:

Корова составлена из пятнадцати спичек. Переложите 2 из них, чтобы получить корову, смотрящую в другую сторону.

Совок с мусором:

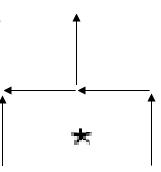
Совок с мусором составлен из 5 спичек. каким образом можно переложить 2 спички, чтобы совок оказался пустым.

Кораблик:

Преобразуйте фигурку «кораблик», сложенную из спичек, в фигурку «ваза», переместив 3 из них.

Забавный треугольник (задача - шутка):

Как с помощью одной спички, не ломая ее, сложить треугольник?

Всего две спички (шутка):

Как с помощью двух спичек, не ломая ее и не расщепляя их, образовать четырехугольник?

В результате знакомства детей с элементами занимательной математики в минуты отдыха может возникнуть у них и интерес к систематическому проведению групповых внеклассных занятий.

Групповые внеклассные занятия по математике проводятся после уроков, но ни по содержанию, ни по форме они не похожи на занятия, которые организуются для отстающих. К внеклассным мероприятиям желательно привлекать всех учеников класса. Каждое из этих занятий планируются учителем в соответствии с требованиями повышения интереса детей к математике и с учетом имеющихся у детей знаний, навыков и умения(некоторые примера таких знаний рассмотрено много выше). Последовательное усложнение содержания заданий проводится, исходя из математики и умений выполнять упражнения из занимательной математики.