Последняя цифра множителя – нечетное число, так как произведение примера оканчивается нечетной цифрой, следовательно, третья цифра второй строки 9. При этом очевидно, что последняя цифра множимого (первая строка) равна3:

Первая цифра множимого 7 или 8; только эти две цифры дают цифру 7 в начале третьей строки при умножении множимого на 9. Используя это положение и то обстоятельство, что четвертая строка трехзначное число, делаем вывод: вторая цифра множителя равна 1.

При умножении на 1 число переписывается без изменения, а тогда число четвертой строки равно числу первой строки и третья цифра третьей строки есть 4.

Число третьей строки делится на 9. Используя признак делимости на 9, находим вторую цифру третьей строки как цифру, дополняющую сумму известных цифр до числа, кратного 9. Так как сумма известных цифр равна: 7+4+7=18, то в качестве неизвестной цифры может быть либо 0, либо 9. Итак, третья строка – 7047 или 7947, а множимое соответственно равно 783 или 883. Но при этом однозначно определилась вторая цифра множимого – 8, а следовательно, и вторая цифра четвертой строки тоже 8.

Четвертая цифра числа шестой строки определяется как последняя цифра суммы второй цифры числа третьей строки, второй цифры числа четвертой строки и четвертой цифры числа пятой строки. Пусть вторая цифра числа третьей строки равна 9. Тогда четвертая цифра числа пятой строки равна 0. Но это невозможно, так как в противном случае множитель начинался бы цифрой 0. Следовательно, вторая цифра числа третьей строки 0, то есть третья строка 7047, множимое примера – 783. Последняя цифра пятой строки 9. Это соответствует тому, что первая цифра множителя 3.

Итоги: 783×319=249777.

Решите самостоятельно:

Квадратики и цифры:

В квадратики впишите по одной цифре так, чтобы выполнялись указанные действия. При этом цифра «нуль» в ребус отсутствует.

Четные и нечетные: В этих примерах буквой «Ч» всюду зашифрованы четные цифры, а буквой «Н» - нечетные. Как выглядит первоначальная запись примеров?

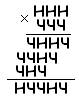
Точные квадраты:

И ВСЕ ЖЕ ОН НЕ ПРАВ

Эта фраза стала предметом глубоких раздумий одного любителя головоломок: можно ли в ней заменить буквы цифрами( одинаковые буквы – одинаковые цифры, разные – разными), чтобы каждое слово стало квадратом некоторого натурального числа?

Подумайте: С помощью математических операций

над этой простой головоломкой, в которой девяти различным буквам соответствует девять различных цифр.

Путешествие:

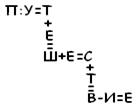
Женские имена:

Уравнение с «иксом»:

Ребусы с ключевыми словами.

В этих ребусах предстоит расшифровать десятибуквенное ключевое слово, которое получиться, если расставите буквы соответственно ух числовому значению от 0 до 9. Разным цифрам соответствуют разные буквы. Между зашифрованными числами поставлены математические знаки, показывающие действия по горизонталям и по вертикалям. Путем рассуждений восстановите числовые значения букв так, чтобы выполнялись указанные действия.

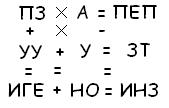
Рассмотрим сумму первого вертикального ряда ПЗ+УУ=ИГЕ. Сумма двух двузначных чисел не больше 198, а, следовательно, И=1.

Из равенства ПЕП – ЗГ =ИНЗ следует, что П = И +1, а поэтому П = 2.

В строке ИГЕ + НО = ИНЗ при сложении Г десятков с Н десяткам получается снова Н десятков. Это означает, что Г = 0(возможен случай Г = 9, но Г≠ 9, так как при сложении не происходит переноса единицы в разряд сотен).

Итак, Г = 0, И = 1, П = 2. А поэтому в равенстве ПЗ + УУ = ИГЕ У принимает значение 7 или 8. Пусть У = 8. В этом случае из равенства УУ + У = ЗТ вытекает, что

Т = 6 и З = 9. Но тогда в разности ПЕП – ЗТ = ИНЗ получаем П = 5, а так как ранее установлено, что П = 2, то делаем вывод: У ≠ 8. Следовательно У = 7, тогда из

УУ + У = ЗТ находим Т = 4, З = 8. Равенство ПЗ +УУ = ИГЕ при З = 8 и У = 7 дает Е = 5.

В сумме ИГЕ +НО = ИНЗ Е = 5, З = 8, а значит, тогда О = 3. В третьем вертикальном ряду известны значения всех букв, кроме одной – Н, поэтому значение этой буквы легко находится: Н = 6. И наконец, в равенстве А × У = Но получаем А = 9.

Математические головоломки.

а) Числовые головоломки – увлекательный тип задач, причем нестандартность и своеобразие этих головоломок начисто отметает какую-либо шаблонность при их решении. Приведенный в условии задач готовый набор чисел, простые числа или квадраты натуральных чисел – отнюдь не гарантирует быстрое, а тем более мгновенное решение.

Как в калейдоскопе, меняя положение нескольких разноцветных стекляшек, можно получить бесконечное множество узоров, так и в числовых головоломках девять натуральных чисел десять цифр от 0 до 9 включительно, причудливо сочетаясь, образуют самые неожиданные задачи – головоломки.

Парангон – специальный термин, которым отмечают бриллиант, драгоценный камень или жемчужину без изъянов. Буквально перевод этого слова – «то, что может служить образом» - в равной степени можно отнести и к большинству числовых головоломок. Хорошую числовую головоломку, подобно драгоценному камню, нетрудно заметить в нагромождении хаоса чисел: ее достоинства проявляются во всем многообразии, заставляя переливаться и сверкать гранями во всем блеске.

Квадраты в квадрате:

Переставьте цифры так, чтобы три образовавших трехзначных числа были точными квадратами.

Магические круги:

Расставьте в меленькие кружки числа от 1 до 10 так, чтобы сумма чисел в четырех больших кругах была равными.

Путешествие по цифрам: