11. В процессе игры должно быть выполнено определённое законченное действие, решено конкретное задание. Игру не следует обрывать незавершенной

Только при этих условиях она оставит след в сознании ребят.

Методические требования к проведению урока – игры.

При организации игр с математическим содержанием необходимо продумать следующие вопросы методики:

1. Цель игры. Какие умения и навыки в области математики дети осваивают в процессе игры. Какому моменту игры надо уделить особое внимание. Какие другие воспитательные цели преследуются при проведении игры (заинтересовать математикой, подготовить детей к организации кружка и так далее).

2. Количество играющих. Каждая игра требует определенного минимального или максимального количества играющих. Это приходится учитывать при организации игр.

3. Какие материалы понадобятся для игры.

4. Как с наименьшей затратой времени познакомить ребят с правилами игры.

5. На какое время должна быть рассчитана игра, учитывая, чтобы дети пожелали еще раз вернутся к этой игре.

6. Как обеспечить более полное участие детей в игре.

7. Как организовать наблюдение за учениками, чтобы выяснить заинтересовала ли их игра.

8. Какие изменения можно внести в игру, чтобы повысить интерес и активность детей.

9. Как можно использовать основу игры, чтобы применить в ней другой математический материал.

10. Какие выводы следует сообщить детям в заключении, после игры(лучшие моменты игры, наиболее активные участники, недочеты в игре и так далее).

III. Занимательная математика в минуты отдыха и на групповых занятиях после урока

Давно установлено, что отдельные упражнения из занимательной математики, математические игры могут доставлять детям такое же удовольствие, так же служить средством разумного отдыха, как и элементы занимательного материала, связанные со спортом, литературой и другими областями науки, искусства. Надо только умело подбирать математические задания, чтобы они вызывали интерес у школьников, ибо возбудить интерес детей к математике – это главная цель, к которой мы стремимся в связи с задачей повышения уровня процесса обучения математике. Для решения этой задачи полезно использовать минуты занимательной математики. С них обычно и зарождается интерес детей к внеклассным занятиям по математике, желание участвовать в работе кружка, в выпуске газеты и других видах работы по математике.

Для проведения минут занимательной математики могут быть использованы отдых в группе продлённого дня, отдельные моменты во время прогулок с группой учащихся, минуты отдыха во время экскурсий, на природе и др.

Для возбуждения и поддержания интереса к заданиям они должны удовлетворять следующим условиям:

1. Быть непохожими на обычные математические задания, предлагаемые на уроках.

2. Смысл заданий должен быть понятен детям.

3. Решение задач должно быть доступно каждому из присутствующих ребят.

4. Ответы должны получаться быстро; если необходимы вычисления, то они должны выполняться только устно.

Минуты занимательной математики проводятся эпизодически. Они могут планироваться учителем в связи с поставленной целью, например возбудить у детей интерес к организации математического кружка, к выпуску газеты и так далее.

Математические ребусы.

К ребусам относят арифметические выражения, обычно записанные в виде равенства, в которых все или некоторые числа заменены символами (буквами, звёздочками, геометрическими фигурами и так далее).

Ребус представляет собой логическую задачу, в которой путём логических рассуждений требуется расшифровать значение каждого символа и восстановить числовую запись выражений.

В Индии и Китае числовые ребусы появились 1000 лет назад. В Европе такие задачи начали появляться в начале XX века, и их назвали крипт – арифметическими.

В настоящее время установились некоторые правила шифровки и дешифровки ребусов.

Так, при шифровке числового равенства буквами разные цифры заменяются разными буквами, а одинаковые цифры заменяются одной и той же буквой. При шифровке ребуса одним символом звёздочка изображает любую из десяти цифр.

По видам шифровки числовые ребусы можно разбить на несколько типов:

1. Все цифры, участвующие в записи числового выражения заменяются буквами. При этом стремятся придать зашифрованной записи какой – либо житейский смысл, желательно оригинальный.

2. Для шифровки числового выражения используются буквы, но при этом часть цифр, участвующих в записи числового выражения заменяют одним символом звёздочкой. Это делается обычно в тех случаях, когда необходимо показать характер промежуточных операций.

Например:

Ясно , что в ребусах такого вида, расшифровав буквы, мы расшифруем весь ребус.

Для шифровки числового выражения используется символ – звёздочка. Примером такой шифровки может служить ребус:

Здесь все цифры, участвующие в ребусе различные. Следует отметить, что в ребусах этого типа или обязательно присутствует хотя бы одна незашифрованная цифра, или все цифры зашифрованы только звёздочкой, но указано некоторое дополнительное условие, например:

Ребусы арифметические.

Арифметические ребусы – примеры обычных арифметических действий (на сложение, вычитание, умножение и деление), в которых все или большая часть цифр заменены звёздочками, кружочками, буквами. В «буквенном» ребусе каждая буква означает одну определённую цифру, в ребусах со звёздочками, квадратиками каждый значок может обозначать любую из десяти цифр – от 0 до 9. Одни цифры могут повторяться несколько раз, а другие вообще оставаться неиспользованными. Расшифровать ребус – это значит восстановить первоначальную запись примера.

При решении задач такого типа требуется внимательность к очевидным арифметическим действиям и умении вести нить логических рассуждений.

Пример №1

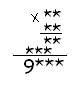
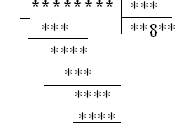
Множимое примера (число, которое умножаем) больше 90. Действительно, если бы множимое было меньше 90, то, умножая его на двузначное число ( множитель), меньше 100, получили бы число, меньше 9000. Но если множимое больше 90, то вторая цифра множителя 1 ( третья строка – двузначное число).

Первая цифра множителя 9. Если допустить, что она меньше 9, например 8, то, умножая на 81 двузначное число (множимое), меньше 100, получим в произведении число, меньшее 8100. Итак, множитель примера равен 91. В качестве множимого возьмём число 98, тогда 98*91=8018. Следовательно, множимое примера – двузначное число, больше 98, то есть 99. Окончательный результат: 99*91=9009.

Пример №2

Так как от умножения множимого (число, меньше 1000) на последнюю цифру множителя получается четырёхзначное число, начинающиеся цифрой (третья строка), то последняя цифра множителя 8 или 9.