Лекции по автоматике

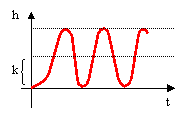
В случаях 1, 2, 3 энергия рассеивалась и колебания затухали, здесь же энергия не рассеивается, а перетекает из одной “емкости” (“емкость” - в универсальном смысле) в другую.

1

2

3

4

x=0

Корни равные, мнимые, комплексно-сопряженные

5. -1<x<0,

1

2

3

4

-1<x<0

Корни комплексно-сопряженные с положительной вещественной частью

Это неустойчивое колебательное звено.

6. x<-1

1

2

3

4

x<-1

Корни вещественные,

разные, положительные

Форма АФХ такая же, как и в случае 5

7. x=-1; отличается от случая 6 лишь тем, что корни одинаковые.

Логарифмические частотные характеристики колебательного звена

Частотная передаточная функция колебательного звена имеет вид откуда при ; при .

Логарифмическая амплитудно-частотная функция имеет вид

1. низкочастотная асимптота имеет наклон 0 дБ/дек;

2. высокочастотная асимптота имеет наклон – 40дБ/дек.

3. обе асимптоты пересекаются на сопрягающей частоте.

При значениях 0,5 < x<1 характеристика близка к ломаной. Если же x<0,5, то получается заметный “горб”. Здесь необходимо вычислять превышение на частоте В упрощенных расчетах достаточно находить

Величина погрешности на сопрягающей частоте для различных x:

при x=1 DL=6,

x=0,5 DL=0,

x=0,1 DL=-14.

Если x от 1 до 0.3, то можно не строить точную ЛАЧХ, а доверитmся асимптотической.

Примеры колебательных звеньев: двигатели постоянного тока, LRC-цепи, регуляторы Уатта и др.

II. Интегрирующие звенья.

Идеальное интегрирующее звено.

Дифференциальное уравнение переходная функция передаточная функция

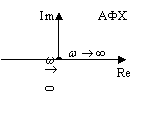Дифференциальное уравнение может быть получено и в такой форме: проинтегрируем это уравнение и получим:

Выведем передаточную функцию:

- размерность передаточного коэффициента; в частном случае, когда входное воздействие и выходная функция имеют одинаковую размерность, [k]=c-1.

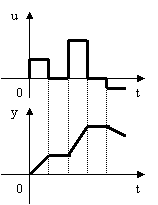
Импульсная переходная характеристика:

Пример. Двигатель постоянного тока, выходная координата которого - угол поворота ротора a¶. Постоянную времени двигателя принять малой и не учитывать.

после интегрирования получим в форме изображений Лапласа