Выходной сигнал нейрона формируется в результате преобразования потенциала нелинейной передаточной функцией f(V). Обычно для этого используется сигмоидальная функция вида

. (2.4.2)

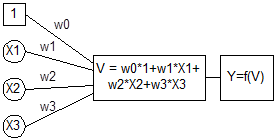
Рис.2.4.1. Математическая модель нейрона.

Объединяя искусственные нейроны в сети, можно получить различные варианты архитектуры. Но в финансовых приложениях чаще всего используются многослойные персептроны (multilayer perceptrons). Это нейронные сети, позволяющие моделировать зависимости между векторами входных и выходных переменных. В многослойных персептронах нейроны объединяются в слои, каждый из которых обрабатывает одинаковые входные сигналы.

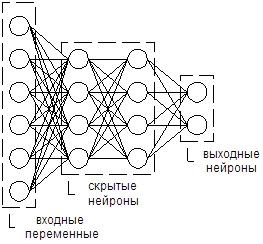
Рис.2.4.2. Архитектура многослойного персептрона.

Входной слой формируют независимые переменные, выходной ­– зависимые. Между ними располагаются скрытые слои. Выходы нейронов предыдущего слоя направляются на вход нейронов последующего слоя. База знаний нейронной сети представляет собой матрицу весов связей между нейронами.

Процесс настройки весов многослойного персептрона называется обучением. Для этого используется обучающая выборка – множество векторов значений объясняющих и объясняемых переменных. Цель обучения заключается в минимизации ошибки оценки объясняемых переменных на основе информации о значениях объясняющих переменных.

Итеративный алгоритм обучения многослойных персептронов, ставший впоследствии классическим и получивший название алгоритма обратного распространения ошибки (error backpropagation), впервые был разработан Полом Вербосом в 1974 г. в рамках работы над магистерской диссертацией в Гарвардском университете[81]. Однако работа Вербоса не была должным образом оценена и долгое время оставалась неизвестной крупнейшим ученым. В 1986 г. алгоритм обратного распространения был заново открыт и популяризирован Д.Румельхартом, Г.Хинтоном и Р.Вильямсом[82]. С начала 1990-х гг. алгоритм обратного распространения стал активно применяться в прикладных разработках.

Алгоритм обратного распространения осуществляет минимизацию функции ошибки, определенной на множестве возможных значений весов сети. Функция ошибки обычно задается как

, (2.4.3)

где 1/2 – константа, введенная для удобства при вычислении производных, i – порядковый номер выходного нейрона, Y ­– размер сигнала выходного нейрона, D – обучающее значение объясняемой переменной.

На каждой итерации работы алгоритма осуществляется переход к новой точке пространства весов сети. Для этого используется метод градиентного спуска, позволяющий выбрать направление, в котором скорость уменьшения значения функции ошибки является максимальной. Коррекция весов производится по правилу

, (2.4.4)

где E – функция ошибки, W – вес, l – коэффициент обучения (размер шага корректировки), t – порядковый номер итерации.

Вычисление производных функции ошибки по весам сети осуществляется по формуле

, (2.4.5)

где j ­– номер нейрона предыдущего слоя, i – номер нейрона последующего слоя, W – вес, V – потенциал, f – передаточная функция.

Производные ошибки по потенциалам вычисляются по правилу цепи, которое и обеспечивает процесс обратного распространения ошибки из нейронов выходного слоя в нейроны предыдущих слоев.

Для выходных нейронов

. (2.4.6)

Для скрытых нейронов

, (2.4.7)

где h ­– номер нейрона последующего слоя, i ­– номер нейрона обрабатываемого слоя.

В целях ускорения процесса обучения часто используется модификация алгоритма обратного распространения, которая обеспечивает большую стабильность процесса корректировки за счет применения оператора экспоненциального сглаживания. В этом случае уравнение обучения принимает вид

, (2.4.8)

где m ­– момент, l – коэффициент обучения.

В ходе обучения сети многократно предъявляется один и тот же набор обучающих примеров. Чем дольше продолжается процесс обучения, тем лучше качество аппроксимации, демонстрируемое сетью при оценке значений выходных переменных по обучающей выборке. Однако через определенное число эпох обучения (под эпохой понимается однократное предъявление сети используемого набора обучающих примеров) улучшение качества аппроксимации начинает обеспечиваться не в результате правильной идентификации нелинейной зависимости между объясняющими и объясняемыми переменными, а за счет точности настройки на специфические особенности обучающих примеров. Этот феномен, получивший название переобучения (overtraining), находит отражение в падении способности сети к обобщению, то есть к адекватной оценке значений выходных переменных по наблюдениям, не предъявленным в ходе обучения.

Для того, чтобы разрешить проблему переобучения, массив исходных данных разбивается на обучающую и тестовую выборки. Обучающая выборка используется в процессе работы алгоритма коррекции матрицы весов сети. Тестовая выборка используется для контроля состояния обученности сети. Процесс обучения прекращается, когда значение ошибки оценки значений выходных переменных по тестовой выборке достигает минимума.

В первой половине 1990-х годов целый ряд исследователей обратился к методологии нейронных сетей как к инструментальному средству анализа финансовых рынков. Однако основные усилия обошли стороной сферу изучения процессов функционирования рынков облигаций. Большинство работ, опубликованных в этот период, посвящены прогнозированию динамики рынков акций и иностранных валют, определению рейтингов кредитоспособности заемщиков, оценке опционов.[83]

Первая попытка разработки нейросетевой модели прогнозирования конъюнктуры рынка облигаций была предпринята В.Ченгом, Л.Вагнером и Ч.Лином[84]. Их усилия были направлены на построение модели, прогнозирующей направление изменения цены тридцатилетней облигации Казначейства США через одну неделю. Используя в качестве объясняющих переменных спот-ставки для различных сроков вложений, индексы рынка акций, денежный агрегат M2, курсы доллара к японской иене и немецкой марке, а также цены на нефть и золото, они сконструировали нейронную сеть, оказавшуюся способной правильно определять направление изменения цены в 67% случаев.

Результаты, полученные Ченгом, Вагнером и Лином, показали, что задача краткосрочного прогнозирования конъюнктуры стабильного высоколиквидного рынка государственных облигаций с использованием нейросетевых моделей вполне разрешима. Однако российский рынок государственных ценных бумаг существенно отличен от американского, что ставит под сомнение возможность эффективного применения нейросетевых алгоритмов в целях поддержки принятия решений по управлению портфелем ГКО–ОФЗ.