сплошной чертой соединены три тройки членов, получаемые параллельным переносом главной диагонали и отвечающие трем слагаемым, входящим в выражение (3.11) со знаком «плюс»; пунктирной же чертой соединены три другие тройки членов, получаемые параллельным переносом побочной диагонали и отвечающие трем слагаемым, входящим в выражение (3.11) со знаком «минус».

1.4. Свойства определителей

Свойство 1. Величина определителя не изменится, если строки и столбцы этого определителя поменять ролями, т.е.

Для доказательства этого свойства достаточно расписать определители, стоящие в левой и правой частях (3.13), по указанному в разд. 1.3 правилу и убедиться в равенстве полученных при этом членов.

Свойство 1 устанавливает полную равноправность строк и столбцов. Поэтому все дальнейшие свойства определителя можно формулировать и для строк, и для столбцов, а доказывать — или только для строк, или только для столбцов.

Свойство 2. Перестановка двух строк (или двух столбцов) определителя равносильна умножению его на число -1.

Доказательство также получается из правила, указанного в предыдущем разделе.

Свойство 3. Если определитель имеет две одинаковые строки (или два одинаковых столбца), то он равен нулю.

Действительно, при перестановке двух одинаковых строк, с одной стороны, определитель не изменится, а с другой стороны, в силу свойства 2 он изменит знак на противоположный. Таким образом, = -, т.е. 2 = 0 или = 0.

Свойство 4. Умножение всех элементов некоторой строки (или некоторого столбца) определителя на число равносильно умножению определителя на это число .

Иными словами, общий множитель всех элементов некоторой строки (или некоторого столбца) определителя можно выносить за знак этого определителя.

Например,

=

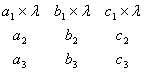Для доказательства этого свойства достаточно заметить, что определитель выражается в виде суммы (3.12), каждый член которой содержит один и только один, элемент из каждой строки и один и только один элемент из каждого столбца.

Свойство 5. Если все элементы некоторой строки (или некоторого столбца) определителя равны нулю, то и сам определитель равен нулю.

Это свойство вытекает из предыдущего (при = 0).

Свойство 6. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю.

В самом деле, в силу свойства 4 множитель пропорциональности можно вынести за знак определителя, после чего остается определитель с двумя одинаковыми строками, равный нулю согласно свойству 3.

Свойство 7. Если каждый элемент п-й строки (или п-го столбца) определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, первый из которых имеет в п-й строке (или в п-м столбце) первые из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах), а второй определитель имеет в п-й строке (в п-м столбце) вторые из упомянутых слагаемых и те же элементы, что и исходный определитель, в остальных строках (столбцах).

Например,

= +

Для доказательства этого свойства снова достаточно заметить, что определитель выражается в виде суммы слагаемых, каждое из которых содержит один и только один элемент из каждой строки и один и только один элемент из каждого столбца.

Свойство 8. Если к элементам некоторой строки (или некоторого столбца) определителя прибавить соответствующие элементы другой строки (другого столбца), умноженные на произвольный множитель , то величина определителя не изменится.

Действительно, полученный в результате указанного прибавления определитель можно (в силу свойства 7) разбить на сумму двух определителей, первый из которых совпадает с исходным, а второй равен нулю вследствие пропорциональности элементов двух строк (или столбцов) и свойства 6.

1.5. Алгебраические дополнения и миноры

Соберем в выражении (3.12) для определителя члены, содержащие какой-нибудь один элемент этого определителя, и вынесем указанный элемент за скобки; величина, остающаяся при этом в скобках, называется алгебраическим дополнением указанного элемента.

Алгебраическое дополнение данного элемента мы будем обозначать прописной латинской буквой того же наименования, что и данный элемент, и снабжать тем же номером, который имеет данный элемент. Например, алгебраическое дополнение элемента будем обозначать через алгебраическое дополнение элемента — через и т. д.