Мы приходим к выводу, что в случае, когда определитель (3.27) отличен от нуля, однородная система (3.25) имеет бесчисленное множество решений, определяемых формулами

, , ,

в которых t принимает какие угодно значения, а алгебраические дополнения , и определяются формулами (3.29).

2.3. Однородная система трех линейных уравнений с тремя неизвестными

Рассмотрим теперь однородную систему трех уравнений с тремя неизвестными:

+ = 0,

++= 0.

Очевидно, что эта система всегда имеет так называемое тривиальное решение: х = 0, у = 0, z = 0.

В случае, когда определитель системы , это тривиальное решение является единственным (в силу разд. 2.1).

Докажем, что в случае, когда определитель равен нулю, однородная система (3.32) имеет бесчисленное множество решений.

Если все определители второго порядка, которые можно составить из матрицы

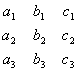
равны нулю, то в силу утверждения из разд. 1.1 соответствующие коэффициенты всех трех уравнений (3.32) пропорциональны. Но тогда второе и третье уравнения (3.32) являются следствиями первого и могут быть отброшены, а одно уравнение ++= 0, как уже отмечалось в разд. 2.2, имеет бесчисленное множество решений.

Остается рассмотреть случай, когда хотя бы один минор матрицы (3.33) отличен от нуля. Так как порядок следования уравнений и неизвестных находится в нашем распоряжении, то, не ограничивая общности, мы можем считать, что отличен от нуля определитель (3.27). Но тогда, как установлено в разд. 2.2, система первых двух уравнений (3.32) имеет бесчисленное множество решений, определяемых формулами (3.31) (при любом t).

Остается доказать, что х, у, z, определяемые формулами (3.31) (при любом t, обращают в тождество и третье уравнение (3.32). Подставляя в левую часть третьего уравнения (3.32) х, у и z, определяемые формулами (3.31), получим

Мы воспользовались тем, что в силу свойства 9 выражение в круглых скобках равно определителю системы (3.32). Но определитель по условию равен нулю, и поэтому при любом t мы получим ++= 0.

Итак, доказано, что однородная система (3.32) с определителем А. равным нулю, имеет бесчисленное множество решений. Если отличен от нуля минор (3.27), то эти решения определяются формулами (3.31) при произвольно взятом t.

Полученный результат можно сформулировать еще и так: однородная система (3.32) имеет нетривиальное решение в том и только в том случае, когда определитель ее равен нулю.

2.4. Неоднородная система трех линейных уравнений с тремя неизвестными с определителем, равным нулю.

Теперь мы располагаем аппаратом для рассмотрения неоднородной системы (3.19) с определителем , равным нулю. Могут представиться два случая: а) хотя бы один из определителей , или - отличен от нуля; б) все три определителя , и равны нулю.

В случае а) оказывается невозможным хотя бы одно из равенств (3.23), т. е. система (3.23) не имеет решений, а поэтому не имеет решений и исходная система (3.19) (следствием которой является система (3.23)).

Переходим к рассмотрению случая б), когда все четыре определителя , , и равны нулю. Начнем с примера, показывающего, что и в этом случае система может не иметь ни одного решения. Рассмотрим систему:

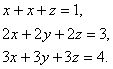
Ясно, что эта система не имеет решений. В самом деле, если бы решение , , существовало, то из первых двух уравнений мы получили бы , , а отсюда, умножая первое равенство на 2, получили бы, что 2 = 3. Далее, очевидно, что все четыре определителя , , и равны нулю. Действительно, определитель системы