Для определения наличия автокорреляции в уровнях этого платежа применяем как универсальный критерий «Дарбина - Уотсона»

d = ,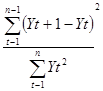

где Y - значение показателей динамического ряда;

t - порядковый номер показателя в динамическом ряде;

n - прогнозный период.

Возможные значения критерия прибывают в интервале 0 – 4. если автокорреляция отсутствует, то значение этого критерия колеблется в рамках числа 2.

Расчёт критерия производится с использованием таблицы.

Таблица 18. Расчёт данных для проверки автокорреляции

млн. грн.

d = 80,3/1204,9 = 0,067

Поскольку значение критерия значительно ниже числа 2, то из этого следует, что взаимосвязь между показателями существует.

Спецификой доходов населения является их определенная инерционность в ежегодном и помесячном повышении, т.е. взаимосвязь в динамике показателей предыдущих и последующих периодов, т.к. формирование фонда оплаты труда как любой экономический процесс является инерционным. Кроме этого для каждого следующего года базисным является фонд оплаты труда предыдущего года.

Поэтому, в любом периоде значение прогнозного показателя поступлений подоходного налога с граждан зависит от фактических его показателей предыдущих периодов. Безусловно, что на прогнозные показатели, когда сравнивать их с предыдущими, влияют разные факторы, те, которые действовали в предыдущие периоды, и новые, что проявляется в прогнозном периоде.

При прогнозировании поступлений подоходного налога сначала можно ограничится от действия новых факторов на прогнозный период, и определить тенденцию изменения этого показателя в предыдущих периодах и на прогнозируемый период.

Значение предыдущих периодов принимаются как факторные для расчёта прогнозных показателей.

Такие тенденции определяются с помощью методов статистического моделирования, в отдельности на основании уравнений регрессии, которые описывают взаимосвязь результативных факторов.

Математически зависимость показателя поступлений подоходного налога с граждан ПНt на прогнозируемый период (t) от фактических показателей предыдущих периодов отображается уравнением линейной зависимости, что выражается формулой:

ПНt = А0 + А1 * ПНt – 1 + А2 * ПНt – 2 + … + Ак * ПНt – к, (1)

где t – порядковый номер, период анализа;

к – прогнозируемый период, к =1,2,3…n;

ПНt – фактическое значение показателя подоходного налога с граждан для периода t;

ПНt – к – фактическое значение показателя подоходного налога с граждан в периоде t - k);

А0, А1, А2…Ак – коэффициенты регрессии.

Достаточной точности прогнозов можно достичь, если в расчётах принять, что к = 13. поэтому на практике целесообразно применять модифицированное уравнение:

ПНt = А0 + А1 * ПНt – 1 + А2 * t (2)

Прогнозируемое значение налога на (t + n) период

ПНt + n = А0 + А1 * ПНt + А2 * (t + n), (3)

где n – прогнозируемый период.

Коэффициенты регрессии А0, А1 и А2 находятся по методу наименьших квадратов.

Для оценки величины ошибки прогноза применяются различные методы анализа качества прогнозов, в отдельности абсолютные показатели ошибки. К таким показателям относится средняя относительная ошибка (Кп).

Для среднесрочных прогнозов (1-5 лет) при Кп, меньше, чем 10, полученные прогнозы будут иметь высокую точность; при Кп = (10-20) – хорошее качество; при Кп = (20-50) – удовлетворительное качество; при Кп больше чем 50 – качество неудовлетворительное.

Поэтому, для оценки объективности расчётов по уравнению (3) следует использовать величину среднего относительного линейного уравнения (Кп), которая вычисляется по формуле:

Кп = 1/j ,

где ПНt – фактическое значение показателя подоходного налога с граждан на период t;

ПНtp – расчетная величина показателя подоходного налога с граждан на период t.

Для примера расчета используем фактические поступления подоходного налога с граждан, которые приведены выше.

Для выполнения расчетов используем таблицу 19.

С учетом определенных по таблице показателей имеем систему нормальных уравнений:

1) 3А0 + 41,67А1 + 6А2 = 54,29

2) 41,67А0 + 1062,6А1 + 89,25А2 = 792,24

3) 6А0 + 89,25А1 + 14А2 = 121,23

Таблица 19. Расчет показателей для составления прогнозов подоходного налога с граждан