Пусть φ – произвольное движение первого рода. Можно считать, что φ ≠ ε. Множество I(φ) в этом случае либо пусто, либо одноэлементно. В первом случае φ – параллельный перенос, во втором – поворот.

Пусть теперь φ – произвольное движение второго рода. Множество I(φ) в этом случае либо пусто, либо является прямой. Это означает, что φ либо скользящая симметрия, либо осевая симметрия. Теорема доказана.

9. Движения как группа геометрических преобразований.

Пусть D – множество всех движений плоскости. На этом множестве определены две операции:

1) операция композиции движений;

2) операция взятия обратного движения.

Будем говорить, что D является группой относительно указанных операций, или группой преобразований.

Кроме множества всех движений плоскости можно указать и другие группы преобразований, например, множество T всех параллельных переносов. А вот множество всех осевых симметрий группой преобразований не является, т.к. композиция двух осевых симметрий – не осевая симметрия. Аналогично, нельзя назвать группой преобразований и множество всех центральных симметрий. Однако можно доказать, что множество S всех центральных симметрий и параллельных переносов, вместе взятых, уже представляет собой группу.

Вообще, множество всех преобразований, которые что-то сохраняют, как нетрудно понять, всегда будет группой, чем бы ни было это «что-то». К таким группам относятся:

- группа всех движений плоскости – они сохраняют расстояния между точками;

- группа преобразований подобия – они сохраняют отношения расстояний;

- группа аффинных преобразований – они сохраняют прямые;

- группа проективных преобразований – они сохраняют прямолинейное расположение точек;

- группа круговых преобразований – они переводят какую-то систему линий в нее же.

Группы преобразований играют в геометрии ключевую роль. Можно даже определить евклидову геометрию как теорию, изучающую свойства фигур, не изменяющиеся под действием элементов группы движений.

С той же точки зрения можно рассматривать и другие, неевклидовы геометрии, которым соответствуют иные группы преобразований. Феликс Клейн поместил понятие группы в фундамент геометрии. Но оно глубоко проникло и в такие области математики, как анализ и комбинаторика, не говоря уже об алгебре. Существует целая наука, изучающая группы, которая так и называется – теория групп. На основе понятия групп была построена топология. Группы стали рабочим инструментом и в таких приложениях математики, как теория кодирования и кристаллография. А некоторых разделов современной теоретической физики, например теории элементарных частиц, просто не существовало бы без теории групп.

Обобщая и подытоживая всё, что изложено выше в данном реферате, можно с уверенностью констатировать:

движения плоскости, т.е. преобразования, сохраняющие расстояние, составляют наиболее важную группу среди всех геометрических преобразований - группу движений плоскости.

10. Применение движений в решении задач.

10.1. Метод параллельного переноса.

Применение каждого преобразования имеет свои особенности. Метод параллельного переноса позволяет сблизить удалённые друг от друга части фигуры и тем упростить задачу.

Рассмотрим, в качестве примера, следующую задачу.

Задача.

Где следует построить мост через реку, разделяющую пункты А и В, чтобы путь l = AP + PQ + QB был кратчайшим? Берега реки считаются параллельными прямыми a и b, а мост, естественно, строится перпендикулярно берегам реки (рис.14).

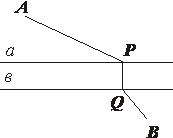Рис.14 Рис.15 Рис.16

Решение.

Заметим, что длина отрезка PQ не зависит от положения точки P на прямой a, а

→ –→

вектор v = PQ определяется лишь прямыми a и b. Поэтому надо найти такое положение точки P, при котором сумма AP +QB будет наименьшей. Пока отрезки AP и QB удалены друг от друга. →

Переведём отрезок AP в положение A’Q параллельным переносом на вектор v.

Получим ломаную A’QB. И теперь становится ясно, что длина ломаной A’QB, а значит и длина l, будет наименьшей в том случае, когда точки A’,Q, B лежат на одной прямой. Итак, Q – точка пересечения отрезка A’B с прямой b, а P – проекция Q на a (рис.15, рис.16).

10.2. Метод поворота.

Рассмотрим, в качестве примера использования метода поворота, следующую задачу.

Задача.

В данном треугольнике ABC найти такую точку, сумма расстояний от которой до вершин треугольника наименьшая.

Решение.

Возьмём в треугольнике ABC любую точку X (рис.17) и рассмотрим сумму

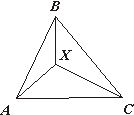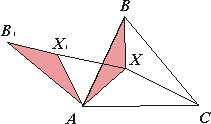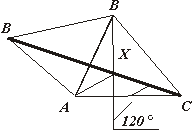Рис.17 Рис.18 Рис.19

Чтобы искать наименьшее значение суммы, надо построить ломаную из отрезков XA, XB, XC. Для этого повернём треугольник ABX вокруг точки А в сторону от треугольника ABC на 60о.Получим: ∆AB’X ’ =∆ABX’ (рис.18).

Рассмотрим ломаную B’X ’XC. В ней B’X’=BX и X’X=XA

(т.к. ∆AXX ’ – равносторонний).

Следовательно, B’X’ + X’X + XC = l.

И становится ясно, что l достигает наименьшего значения тогда, когда точки X’ и X лежат на отрезке B’C. (Заметим, что положение точки B’ определено – она вершина равностороннего треугольника ABB’).