, и условия теоремы 1 не выполнены. Тот же результат получается по формуле (4) при h=0:

.

Т.к. на оси Ox имеем , то решения по оси удаляются от точки (0, 0) со скоростью 1 и решение неустойчиво

§2. Некоторые сведения теории дифференциальных

уравнений с импульсным воздействием.

При математическом описании эволюции процессов с кратковременными возмущениями часто длительностью возмущения пренебрегают и считают, что эти возмущения носят “мгновенный” характер. Такая идеализация приводит к необходимости исследовать динамические системы с разрывными траекториями или, как их еще называют, диф. уравн. С импульсным воздействием.

Определение таких систем приведено [12], они задаются

а) системой диф. уравн.

(5)

б) некоторым множествам Ft, заданным в расширенном фазовом пространстве,

в) оператором At, заданным на множестве Ft и отображающем его на множество .

Сам процесс происходит следующим образом: изображающая точка , выйдя из точки (t0, x0), движется по кривой {t, x(t)}, определяемой решением x(t) = x(t, t0, x0) системы уравнений (1). Движение по этой кривой осуществляется до момента времени t = t1 > t0, в который точка (t, x(t)), встречается с множеством Ft (попадает в точку множества Ft). В момент времени t = t1 точка Pt “мгновенно” перебрасывается оператором At из положения в положение и движется дальше по кривой {t, x(t)}, которая описывается решением системы уравнений (1). Движение по указанной кривой происходит до момента времени t2 > t1, в которой точка Pt снова встречается с множеством Ft. В этот момент под действием оператора At точка Pt мгновенно перескакивает из положения в и движется дальше по кривой {t, x(t)}, описываемой решением системы уравнений (1), до новой встречи с множеством Ft и т.д.

Совокупность соотношений а) – в) называют системой диф. уравнений с импульсным воздействием.

Кривую {t, x(t)} описываемую точкой Pt называют интегральной кривой, а функцию x = x(t), которая задает эту кривую – решением системы (1).

Систему диф. уравнений с импульсным воздействием (совокупность соотношений а)- в)) можно записать в более компактной форме:

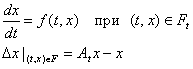(6)

Т.о., решение системы уравнений (2) - это функция, удовлетворяющая уравнению (5) вне множества Ft и имеющая разрывы первого рода в точках Ft со скачками

- состояние системы до и после скачка в момент времени t1.

В зависимости от характера импульсного воздействия выделяют несколько видов таких уравнений. Рассмотрим систему с нефиксированными моментами импульсного воздействия, т.е. системы, подвергающиеся импульсному воздействию в момент попадания изображающей точки Pt на заданные поверхности расширенного фазового пространства. Тогда система (6) примет вид:

(7)

Устойчивость в системах с нефиксированными моментами

импульсного воздействия.

Определение 2.

Решение x(t) системы уравнений (7), определенное при всех t≥t0, называется устойчивым по Ляпунову, если для произвольных чисел и существует такое число , что для любого другого решения y(t) уравнений (7) из того , что следует, что при всех t≥t0 таких, что , где – моменты пересечения интегральной кривой решения x(t) поверхностей .

Определение 3.

Решение x(t) системы уравнений (7) называется асимптотически устойчивым, если оно устойчиво в определенном выше смысле и если можно указать такое число , что для любого другого решения этой системы уравнений, удовлетворяющего неравенству имеет место предельное равенство: .

Вопрос исследования устойчивости некоторого решения уравнения (7), как и в случае обыкновенных диф. уравнений, можно свести к вопросу исследования устойчивости тривиального решения некоторой новой системы уравнений с импульсным воздействием. Эта процедура описана в [12], в результате которой получим систему диф. уравн. с импульсным воздействием:

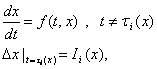(8)

где т.е. решение x=x(t) системы (7) перешло в положение равновесия системы (8).

Вопрос устойчивости нулевого решения системы (8) можно решить с помощью прямого метода Ляпунова (метод функций Ляпунова).

Теорема 3.

Если существует положительно-определенная функция, удовлетворяющая в некоторой области D неравенствами

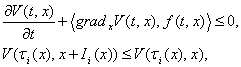(9)

то тривиальное решение системы уравнений (8) устойчиво.

Если же вместо второго из неравенств (9) потребовать, чтобы выполнялось неравенство

для всех - непрерывная при функция, , то нулевое решение уравнений (8) асимптотически устойчиво.