Т.о., существование теории релейных систем, систем переменной структуры, реализация законов оптимального управления, механики, электротехники приводят к необходимости изучения общей теории диф. уравн. с разрывными правыми частями, для которых в общем случае неприемлемы методы классической теории дифференциальных уравнений.

§2. Обзор работ по теории дифференциальных уравнений с разрывными правыми частями.

Различным вопросам этой теории посвящены отдельные параграфы и главы в книгах [3,4,7,9], а также большое число журнальных статей.

Систематическое изложение этой теории имеется в статьях А.Ф. Филиппова. В [16] Филиппов рассмотрел диф. уравн. с однозначными разрывными правыми частями, ввел понятие решения и доказал основные теоремы качественной теории.

Различные направления исследования релейных диф. уравн. , т.е. таких уравнений, у которых правая часть не является ненпрерывной по x функций рассмотрены в статье [5].

Теория систем автоматического управления, описываемых дифференциальными уравнениями с разрывными правыми частями рассматривается в книгах [13, 14, 15]. В работе С.В. Емельянова [13] излагается один из разделов теории автоматичесеого управления – теория систем с переменной структурой, принадлежащих к классу нелинейных систем автоматического регулирования, в которых широко используются скользящие режимы. Скользящие режимы релейных систем изучались Ю.И Неймарком [10], Ю.И. Алимовым [2] и др. Но появление систем с переменной структурой породило интерес к теории скользящих режимов не только в релейных системах общего вида [14, 15]. Содержание последних книг составляют проблемы, связанные с исследованием систем с разрывными управляющими воздействиями, в [14] приводится математический аппарат для исследования разрывных динамических систем, которые не рассматриваются в классической теории диф. уравнений. Обзор и основные направления теории диф. уравнений с разрвными правыми частями приводятся в книге [17], которая явилась основной при написании дипломной работы.

Во всех вышеперечисленных работах теория разрывных систем основывается на теории дифференциальных включений. Нами было сделано предположение, что эти системы можно свести к системам дифференциальных уравнений с импульсным воздействием, теория которых изложена в [12]. Для этого потребуется дать определения решения, устойчивости решения разрывной системы в смысле системы с импульсным воздействием, сформулировать теорему об устойчивости нулевого решения.

Глава II

Определения решения дифференциального уравнения с разрывной правой частью.

Здесь из лагаются различные определения решений дифференциальных уравнений с разрывными правыми частями, устанавливается связь таких уравнений с дифференциальными включениями, указываются условия их применимости.

§1. Обоснование необходимости обобщения понятия

решения дифференциального уравнения.

Определение1. Решением дифференциального уравнения

=

с непрерывной правой частью называется функция , которая всюду на данном интервале имеет производную и удовлетворяет этому уравнению.

Для дифференциальных уравнений с разрывными правыми частями такое определение непригодно, как показывают следующие примеры.

Пример 1.

При =-1 и решение выражается формулой ;

при , решение :

Исходя из требования непрерывности решения при :

x(0)=,

. Поэтому решение выражается формулой . При производной не существует.

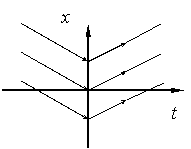
Пример 2.

При 3, решение ,

при , решение :

x

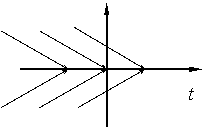
При возрастании каждое решение доходит до прямой 0. Поле направлений не позволяет решению сойти с прямой 0 ни вверх, ни вниз. Если же продолжить решение по этой прямой, то получаемая функция не удовлетворяет уравнению в обычном смысле, т.к. для нее, а правая часть уравнения при равна 1-sign 0=10.

Кроме этого, уравнение с непрерывной правой частью равносильно интегральному уравнению

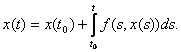
В случае, когда f(t,x) разрывна по t и непрерывна по x (пример 1), решением уравнения можно назвать функции, удовлетворяющие интегральному уравнению. В этом случае, решения с одной стороны от S подходят к S, а с другой стороны сходят с S (траектории “прошивают” поверхность):