Такое определение дает однозначное продолжение решения по поверхности разрыва.

Рассмотрим случай, когда функция разрывна на гладкой поверхности , задаваемой уравнением . Поверхность S делит свою окрестность в пространстве на области и . Пусть при и приближении к из областей и функция имеет предельные значения

Тогда множество , о котором говорится в доопределении А, есть отрезок, соединяющий концы векторов и , проведенных из точки .

aЕсли этот отрезок при лежит по одну сторону от плоскости , касательной к поверхности в точке, то решения при этих переходят с одной стороны поверхности на другую:

Рис. 1.

aЕсли этот отрезок пересекается с плоскостью , то точка пересечения является концом вектора , определяющего скорость движения

(3)

по поверхности в пространстве :

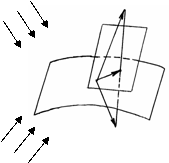
Рис. 2.

Причем касательный вектор к S , следовательно . Это значит, что функция , удовлетворяющая уравнению (3) в силу доопределения А считается решением уравнения (1). Разумеется, непрерывная функция , которая на данной части рассматриваемого интервала времени проходит в области (или в ) и там удовлетворяет уравнению (1), а на оставшейся части проходит по поверхности и удовлетворяет уравнению (3), также считается решением уравнения (1) в смысле доопределения А.

В уравнение (3) ,

, ( ),

- проекции векторов и на нормаль к поверхности в точке (нормаль направлена в сторону области ).

Вместе с тем множество F(t, x) можно было определить иначе. В качестве) возьмем произвольное ограниченное выпуклое множество, содержащее отрезок J:

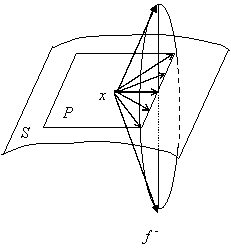
Рис. 3.

При этом на касательной плоскости появляются векторы, отличные от ; это приводит к тому, что кроме решения Филиппова появляются и другие решения.

Т.о. определение (А) А.Ф. Филиппова соответствует минимальному возможному определению множества F(t, x) среди всех допустимых. Это удобно в том отношении, что для решения в смысле Филиппова чаще, чем в других случаях, имеет место единственность решения.