Найдём, например, угол между диагоналями А¹В и В¹С граней нашего куба (рис. 14). Заме­ним прямую В¹С на параллельную ей диагональ A¹D противоположной грани; искомый угол равен углу BA¹D, т. е. 60° (треугольник BA¹D равносторонний). Угол между диагональю АС¹ и основанием куба равен углу САС¹ между прл* мой ас¹ и её проекцией АС на основание, т.е. arctg (C¹C/AC) = arctg (1/√2]. А угол между пло­скостями BDA¹ и BDC¹ (рис. 14) равен углу А¹МС¹, где М — середина BD, так как прямые МА¹ и МС¹ лежат в этих плоскостях и перпендикулярны их линии пересечения BD (несложное вычисление даёт arccos (1/3)).

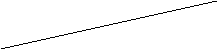
Расстоянием между двумя любыми фигура­ми называют наименьшую длину отрезка, концы которого принадлежат данным фигу­рам. Значит, расстояние от точки до плоскости равно длине перпендикуляра, опущенно­го из точки на плоскость, — он короче любой наклонной, так как гипотенуза прямоугольно­го треугольника короче катета. Расстояние между параллельными плоскостями, очевидно, равно расстоянию от любой точки в одной из них до другой плоскости (рис. 15, а).

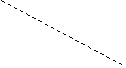
Более интересен вопрос о расстоянии между двумя скрещивающимися прямыми а и b. Проведём через прямую а плоскость α, параллельную прямой b (рис. 15, б), найдем точку пересечения А ортогональной проекции b¹ прямой b на α и точку В прямой b, которая проектируется в точку А. Отрезок АВ перпендикулярен плоскости а и потому является общим перпендикуляром к прямым а и b. Его длина и

б

а

b

равна расстоянию между нашими скрещивающимися прямыми.

b¹

a

α

A

Вместо того чтобы вычислять расстояния и углы в пространстве, часто можно находить соответствующие величины на ортогональной проекции данной фигуры. На рис. 15 показаны .те интересные ортогональные проекции куба '„' ребром длины и: прямоугольник размером

а * а√2 (проекция на диагональную плоскость АСС¹А¹ или, что то же, вдоль диагонали BD ос­нования): и правильный шестиугольник со сто­роной а√2/3 (проекция вдоль диагонали куба АС¹; мы видели, что прямая АС¹ перпендику­лярна плоскости BDA¹, а потому правильный треугольник BDA, со стороной а√2 в такой проекции не искажается). С помощью первой проекции можно найти, например, угол между плоскостями BDA¹ и BDC¹ — он равен углу меж­ду красными прямыми, в которые проектиру­ются эти плоскости. А расстояние r между двумя скрещивающимися диагоналями граней BD и В¹С равно расстоянию на рис. 16, а от точки В до прямой В¹С (В и B¹C — изображения первой и второй диагоналей соответственно). Поду­майте почему. (Здесь важно, что общий перпендикуляр диагоналей параллелен плоскости про­екции.) Легко найти, что r= а/√3. Нетрудно вычислить на той же проекции и расстояние между прямыми BD и АС¹ Ещё проще найти его с помощью рис. 16, б, на котором АС¹ превра­щается в точку: расстояние от последней — центра шестиугольника — до BD равно половине стороны шестиугольника, т. е. а/√6.

б

B¹

B

A¹