До сих пор мы, по существу, нигде не пользовались такими важными геометрическими понятиями, как расстояния и углы. Даже в нашем кубе нам достаточно было только того, что его грани- параллелограммы, равенства всех их сторон и углов на самом деле не требовалось. Чтобы иметь возможность изучать свойства куба и других пространственных фигур во всей полноте, нужны соответствующие определения. Прежде всего, расширим понятие перпендикулярности, известное из планиметрии.
Если прямая пересекает плоскость в этой плоскости, проходящей через точку Р, то говорят , что данные прямая и плоскость перпендикулярны.
Например, ясно, что ребро АА¹ нашего куба перпендикулярно основанию АВСD. Но как проверить, что это ребро действительно перпендикулярно любой прямой, лежащей в основе и проходящей через А? Оказывается, достаточно того, что АА¹ составляет прямые углы с двумя из них – АВ и АD: согласно признаку перпендикулярности прямой и плоскости,
· Если прямая l перпендикулярна двум пересекающимся прямым a и b, то она перпендикулярна плоскости, содержащей a и b.
Причём здесь не обязательно предполагать, что прямые a и b пересекают l: считают, что скрещивающиеся прямые перпендикулярны, если перпендикулярны параллельные им прямые, проходящие через произвольно взятую точку, в частности через точку пересечения l с плоскостью. Так что теперь можно сказать, что прямая, перпендикулярная плоскости, перпендикулярна любой лежащей в этой плоскости прямой. Справедлива такая теорема:
· Через данную точку в пространстве можно провести одну и только одну плоскость, перпендикулярную данной прямой, а также одну и только одну прямую, перпендикулярную данной плоскости.
Параллельная проекция на плоскость вдоль перпендикулярной ей прямой называется ортогональной (т. е. прямоугольной) проекцией на данную плоскость. Обычно, когда говорят просто «проекция», имеют в виду именно ортогональную проекцию. Она обладает всеми общими свойствами параллельной проекции. Но у неё есть и специфические свойства, их можно использовать при решении задач о расстояниях и углах в пространстве.
 Из признака перпендикулярности прямой и плоскости выводится очень простая, но важная теорема о трёх перпендикулярах (рис. 11):
Из признака перпендикулярности прямой и плоскости выводится очень простая, но важная теорема о трёх перпендикулярах (рис. 11):
· 
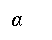
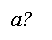




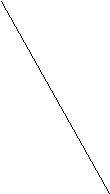


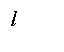
Наклонная a к плоскости перпендикулярна к прямой l в этой плоскости тогда, когда её проекция а¹ на плоскость перпендикулярна l.
Наклонной к плоскости называют любую пересекающую её, но не перпендикулярную ей прямую. Оба условия в этой теореме равносильны тому, что плоскость, содержащая а и а', перпендикулярна прямой /.

Применим обе теоремы к кубу (рис. 11). Проекция АС его диагонали АC¹ на основание перпендикулярна диагонали основания BD; по теореме о трёх перпендикулярах, и сама диагональ АС¹ перпендикулярна BD. По такой же причине перпендикулярны АС¹ и А¹В. Отсюда следует, что диагональ перпендикулярна «треугольному сечению» A¹BD.
В стереометрии помимо обычных плоских















углов приходится иметь дело ещё с тремя видами углов. Угол между скрещи-вающимися прямыми, по определению, равен углу между пересекающимися прямыми, которые им параллельны. Угол между прямой а и плоскостью о. равен углу между прямой а и её проекцией а' на плоскость (рис. 10), а если прямая и плоскость перпендикулярны, его принимают равным 90°. Это наименьший из углов между прямой а и любой прямой в плоскости а. Угол между пересекающимися плоскостями измеряется углом между перпендикулярами, проведёнными в этих плоскостях к линии их пересечения (рис. 13). Все названные углы принимают значения в промежутке от 0

























до 90°.
![]() Из признака перпендикулярности прямой и плоскости выводится очень простая, но важная теорема о трёх перпендикулярах (рис. 11):
Из признака перпендикулярности прямой и плоскости выводится очень простая, но важная теорема о трёх перпендикулярах (рис. 11):

![]()
![]()
![]()
![]()
![]()


![]()

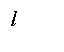
![]()
 Применим обе теоремы к кубу (рис. 11). Проекция АС его диагонали АC¹ на основание перпендикулярна диагонали основания BD; по теореме о трёх перпендикулярах, и сама диагональ АС¹ перпендикулярна BD. По такой же причине перпендикулярны АС¹ и А¹В. Отсюда следует, что диагональ перпендикулярна «треугольному сечению» A¹BD.
Применим обе теоремы к кубу (рис. 11). Проекция АС его диагонали АC¹ на основание перпендикулярна диагонали основания BD; по теореме о трёх перпендикулярах, и сама диагональ АС¹ перпендикулярна BD. По такой же причине перпендикулярны АС¹ и А¹В. Отсюда следует, что диагональ перпендикулярна «треугольному сечению» A¹BD.
![]()
![]()












 углов приходится иметь дело ещё с тремя видами углов. Угол между скрещи-вающимися прямыми, по определению, равен углу между пересекающимися прямыми, которые им параллельны. Угол между прямой а и плоскостью о. равен углу между прямой а и её проекцией а' на плоскость (рис. 10), а если прямая и плоскость перпендикулярны, его принимают равным 90°. Это наименьший из углов между прямой а и любой прямой в плоскости а. Угол между пересекающимися плоскостями измеряется углом между перпендикулярами, проведёнными в этих плоскостях к линии их пересечения (рис. 13). Все названные углы принимают значения в промежутке от 0
углов приходится иметь дело ещё с тремя видами углов. Угол между скрещи-вающимися прямыми, по определению, равен углу между пересекающимися прямыми, которые им параллельны. Угол между прямой а и плоскостью о. равен углу между прямой а и её проекцией а' на плоскость (рис. 10), а если прямая и плоскость перпендикулярны, его принимают равным 90°. Это наименьший из углов между прямой а и любой прямой в плоскости а. Угол между пересекающимися плоскостями измеряется углом между перпендикулярами, проведёнными в этих плоскостях к линии их пересечения (рис. 13). Все названные углы принимают значения в промежутке от 0 














 до 90°.
до 90°.
