Хроматическая дисперсия связана с удельной хроматической дисперсией простым со­отношением:

(3.2.12)

К уменьше­нию хроматической дисперсии ведет использование более когерентных источников излучения, например лазерных передатчиков, и использование рабочей длины волны более близкой к длине волны нулевой дисперсии.

3.3. Распространение световых импульсов в среде с дисперсией

Электрическое поле линейно поляризованного светового сигнала, распространяющегося в одномодовом волокне, можно описать следующим образом [6]:

, (3.3.1)

где - единичный вектор, - медленно меняющаяся амплитуда (огибающая) светового импульса, представляющая собой комплексный скаляр, который изменяется в направлении z и во времени t, u(х,у) - распределение амплитуды поля в поперечном направлении, - постоянная распространения, - угловая частота.

Распределение амплитуды поля основной моды в поперечном направлении описывается следующим уравнением [6]:

, (3.3.2)

где (ω)- диэлектрическая проницаемость среды.

В отсутствие в волокне нелинейных явлений рассчитать изменение формы светового импульса в процессе распространения вдоль волокна можно, воспользовавшись преобразованием Фурье [6].

Рассмотрим распространение спектральных компонент светового сигнала , получаемых преобразованием Фурье огибающей светового импульса :

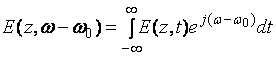, (3.3.3)

где - несущая частота.

Спектральные компоненты удовлетворяют уравнению:

, (3.3.4)

где - коэффициент затухания сигнала, =.

Решение этого уравнения известно и характеризует затухание сигнала и сдвиг фаз, пропорциональный пройденному расстоянию:

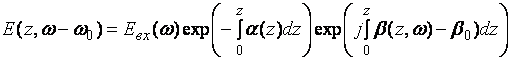,(3.3.5)

где Фурье - образ входного светового сигнала имеет вид:

, (3.3.6)

Для однородного волокна выражение упрощается:

(3.3.7)

Как следует из выражения (3.3.7), в процессе распространения по волокну разные спектральные компоненты приобретают различный фазовый сдвиг, поэтому Фурье - образ выходного сигнала, прошедшего участок однородного ОВ длиной L, имеет вид:

. (3.3.8)

Форма выходного сигнала может быть получена из Фурье - образа обратным преобразованием Фурье:

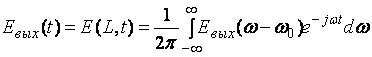. (3.3.9)

Искажение световых импульсов при распространения в ОВ можно оценить, разложив постоянную распространения β(ω) в ряд Тейлора около несущей частоты [6]:

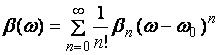, (3.3.10)

где:

(3.3.11)

Выражение (3.3.10), ограниченное первыми четырьмя членами разложения, имеет вид:

. (3.3.12)

Если в разложении (3.3.12) пренебречь степенями выше первой, что соответствует распространению светового импульса по ОВ без искажений, то после подстановки (3.3.12) в (3.3.8), (3.3.9) получается:

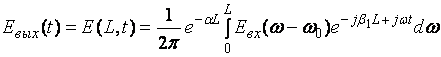. (3.3.13)

Сделав замену переменных , получим . Т.е. в рассмотренном приближении световой импульс затухает, форма его не меняется, и на выходе из волокна он оказывается с временной задержкой . Следовательно, групповая скорость распространения светового импульса равна .

Обычно коэффициент при квадрате разности частот не равен нулю, в этом случае световой импульс искажается. Для светового импульса произвольной формы получить аналитическое выражение не удается, но для импульса гауссовой формы () аналитическое выражение для выходного импульса имеет следующий вид:

, (3.3.14)

где - начальная длительность импульса.

Таким образом, гауссовский импульс сохраняют свою форму, но его длительность , увеличивается [7]:

, (3.3.15)

где величина называется дисперсионной длиной. Выражение (3.3.15) показывает, что при импульс расширяется. Темп расширения импульса определяется дисперсионной длиной . При определенной длине световода более короткий импульс уширяется больше, т.к. его дисперсионная длина меньше. При z = гауссовский импульс уширяется в раз. Импульс, вначале не имевший частотной модуляции, приобретает ее по мере распространения в ОВ.

Из выражения (3.3.15) следует, что уширение гауссовского импульса, не обладавшего на входе частотной модуляцией, не зависит от знака параметра дисперсии . Поведение изменяется, однако, если импульс на входе имеет некоторую частотную модуляцию. В случае линейной частотной модуляции гауссовского импульса амплитуда огибающей записывается в виде [6]:

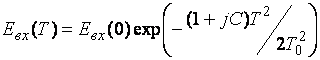, (3.3.16)

где С - параметр модуляции. Полуширина спектра (на уровне интенсивности 1/е от максимальной) определяется выражением: