Буферное действие диатомита в системе твёрдая фаза – раствор

Проведённые эксперименты показали, что порошок диатомита влияет на реакцию раствора извлечения: он повышает значения рН кислых растворов, щелочных же, напротив, понижает. Буферное действие породы гораздо сильнее проявляется в кислой среде, причём нативный диатомит воздействует на величину рН раствора гораздо эффективнее диатомита, прокалённого при 850°С: для него максимальное значение │ΔрН│составило 4,34 при рНисх =2,7. Подвергнутый термообработке диатомит способен изменять рН раствора извлечения максимум на 1,95 единицы рН при рНисх=3,12.

При исследовании влияния порошка нативного диатомита на концентрацию Al3+ в растворах AlCl3 (исходное значение СAl3+ 0,0086 мг/см3) с различными значениями рН были получены данные, особенно ярко демонстрирующие его буферное действие в интервале значений рН 1,4-12,38, особенно в щелочной среде.

Результаты исследований приведены в таблицах 2.14, 2.15 и 2.16 и отражены на графиках, приведённых на рисунках 2.9, 2.10 и 2.11.

Таблица 2.14

Влияние порошка нативного диатомита на величину рН раствора извлечения (1 М раствора KCl c установленным значением рН)

рН исх	1,02	1,94	2,70	4,01	6,07	8,30	9,60
ΔрН	-0,45	-1,48	-4,34	-1,66	-1,19	0,82	1,12

Таблица 2.15

Влияние порошка нативного диатомита на величину рН раствора извлечения (раствора AlCl3 c установленным значением рН)

Таблица 2.16

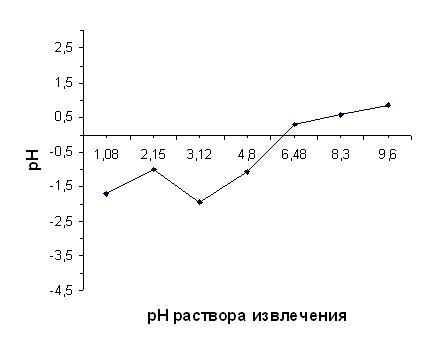
Влияние порошка диатомита, прокалённого при 850°С,

на величину рН раствора извлечения (1 М раствора KCl c установленным значением рН)

рН исх	1,08	2,15	3,12	4,80	6,48	8,30	9,60
ΔрН	-1,71	-0,98	-1,95	-1,07	0,30	0,57	0,85

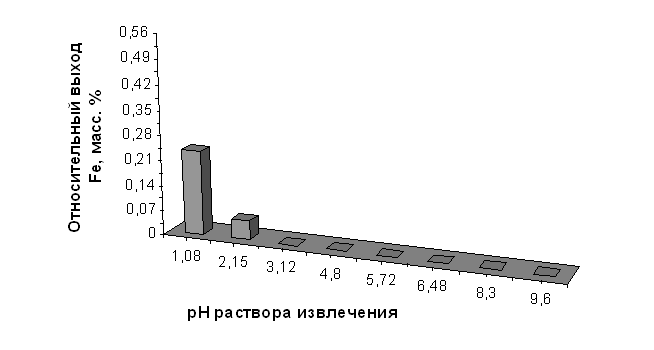
Буферное действие диатомита в кислой среде связано:

· с адсорбцией протонов на сколах частиц алюмосиликатов и последующим разрушением их кристаллической решётки;

· с адсорбцией ионов H+ на гидроксилированной поверхности опалового кремнезёма за счёт сил ионного притяжения вплоть до рН~2, при котором число заряженных центров на поверхности кремнезёма равно нулю (точка нулевого заряда).