Формула (80) – формула Дини-Шварца или интегральная формула Дини-Шварца для кругового кольца.

Если в равенстве (79) отделить действительные и мнимые части, то мы получим непосредственное обобщение интегральной формулы Дини, дающее решение граничной задачи Неймана для кругового кольца:

(89)

,

,

где , , .

Формулу (81) можно назвать формулой Дини-Вилля для кругового кольца.

Аналогично можно найти интегральные формулы Пуассона, Шварца-Дини для любых () связных (конечных и бесконечных) областей, используя формулы (70) и (71).

§6. Интегральная формула Чизотти-Пуассона-Дирихле

для конечных трехсвязных областей.

Формула Чизотти для многосвязных круговых областей дает выражение функции, реализующей конформное отображение области ограниченной окружностями , (, 0, 1, 2 и ) на многосвязную область плоскости , ограниченную гладкими кривыми .

Если в каждой точке , где , контура области плоскости известен угол наклона касательной к , где , - внешняя, - внутренние, , .

Построим функцию дающую конформное отображение области на , где . тогда голоморфна в и действительная часть голоморфной функции равна на окружности , т.е.

, , (90)

где - угол наклона касательной к в точках соответствующих при отображении функцией .

Из существования отображающей функции следует, что функция в области согласно (82) можно представить по формуле Шварца для многосвязных областей. Функция регулярна и однозначна в области и ее действительная часть на принимает непрерывные значения . Тогда с помощью формулы Шварца, с учетом (82) функция принимает вид:

, (91)

где , , , - заданная плотность по граничному условию (81), - ядро, определяемое следующими формулами:

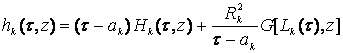, где:

;

(92)

;

;

; ; .

; ,

где ядра, зависящие от натурального параметра.