Тогда, применяя введённую им функцию П(х), он получает зависимости, позволяющие по сторонам треугольника вычислять его углы. И оказывается, что в любом треугольнике сумма внутренних углов меньше 180°. Значит, в четырёхугольнике Саккери (если разбить его диагональю на два треугольника; рис. 19) сумма углов меньше 360°.

Это означает, что мы находимся в условиях гипотезы острого угла – когда в четырёхугольнике Саккери угол φ<90°. Как будто ничего нового нет: Саккери и его последователи так и не нашли противоречия в гипотезе острого угла.

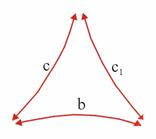Однако Лобачевский оказался теперь намного богаче: он имел формулы, выражающие зависимости между сторонами и углами треугольника. Пользуясь своими зависимостями, Лобачевский доказал: если известны углы треугольника, можно однозначно вычислить его стороны. Однако существуют подобные треугольники, в которых при равных углах стороны могут отличаться по длине сколь угодно сильно.

Казалось бы – вот оно, желанное противоречие. Но наличие подобных, но неравных друг другу треугольников доказывается с помощью аксиомы о параллельных прямых. А потому сам факт, что такие треугольники существуют, может рассматриваться как ещё одна новая аксиома, эквивалентная пятому постулату.

И тогда Лобачевский сделал вывод: противоречия не будет никогда. Иначе говоря, если мы добавляем ко всем прочим аксиомам ещё и пятый постулат, то получается непротиворечивая (см. гл. «Введение», стр. 3; «Аксиоматика Гильберта», прил. «Доказательство непротиворечивости аксиоматики Гильберта», стр. 11) геометрическая система – привычная нам евклидова геометрия; если же мы присоединим к остальным аксиомам утверждение, отрицающее пятый постулат, то получим другую геометрическую систему («Воображаемую» геометрию по Лобачевскому), которая тоже непротиворечива.

Однако доказать непротиворечивость своей системы, построить её модель на материале евклидовой геометрии Лобачевскому не удалось. Учёный умер, так и не добившись признания своих идей. Гаусс, не решившись поддержать Лобачевского, добился, однако, избрания его членом-корреспондентом Гёттингенского учёного общества. Это была единственная почесть, возданная Лобачевскому как учёному при жизни.

Первая работа Лобачевского, посвященная этому вопросу вышла в 1826 году. Позднее, в 1840 году, им была опубликована работа «Геометрические исследования по теории параллельных линий». Незадолго до смерти им была написана работа, подводившая итог его исследованиям, – «Пангеометрия».

Фаркаш же Бойяи был другом Гаусса ещё по Гёттингену, и можно полагать, что они обсуждали проблему параллельных линий. Более того, два раза, в 1804 и 1808 году, Бойяи писал Гауссу о трудностях в поиске доказательства постулата о параллельных. Гаусс, обнаружив у него ошибки, ничего не ответил. Ф. Бойяи, впав в меланхолию от безрезультатных поисков ответа на этот вопрос, и занялся сочинением стихов и пьес. Его сын, Янош унаследовал от отца интерес к проблеме параллельных линий. Сначала он продолжал исследования отца, но затем стал склоняться к мысли о недоказуемости пятого постулата. В 1823 году он сформулировал идею неевклидовой геометрии и 23 ноября сообщил отцу о намерении опубликовать результаты своих исследований. Именно в это время Лобачевский в Казани, Гаусс в Гёттингене, Тауринус в Кёльне также находились на пороге великого открытия. Однако работа Бойяи не была опубликована до 1832 года.

Сочинение Лобачевского «Геометрические исследования…» стало известно ему в 1848 году. Тогда он предпринял своего рода рывок, стремясь завершить большую работу по теории пространства, задуманную им ранее. Однако значительная часть его работы представляла собой нагромождение различных черновых набросков, не до конца осознанных и отработанных идей. Его стремление превзойти русского соперника осталось неосуществлённым.

Сегодня является общепризнанным, что Бойяи, Лобачевский и Гаусс одновременно и независимо друг от друга открыли неевклидову геометрию, т. е, по сути непротиворечивую систему основывающуюся на своей непротиворечивой аксиоматике.

Однако вызывает удивление тот факт, что неевклидова геометрия рассматривалась лишь в пределах гипотезы острого угла. Неевклидова геометрия, основанная на гипотезе тупого угла была рассмотрена Риманом в 1854 году. В его новой геометрии на сферической поверхности любые две линии пересекаются.

Позже математикам (Клейну, Кэли, Пуанкаре и др.) удалось создать модель геометрии Лобачевского на материале евклидовой, и, таким образом, доказать непротиворечивость и законность новой геометрии. Часто встречающиеся в литературе названия геометрии Лобачевского – «гиперболическая», Римана – «эллиптическая» и евклидовой – «параболическая» принадлежат Клейну.

Гаусс пытался выяснить, какова геометрия реального пространства Вселенной – гиперболическая, эллиптическая или параболическая. Для этого необходимо было ответить на вопрос, какова сумма внутренних углов треугольника. Известно, что Гаусс, будучи научным руководителем астрономической обсерватории, проводил измерения углов треугольников, образованных вершинами гор[2]. Однако он не вполне отдавал себе отчёт в том, сколь значительны неизбежные погрешности таких измерений.

Открытие неевклидовой геометрии было первым ударом по взглядам на аксиомы, как на вечные и непреложные, «априорные» истины.

Вместе с тем, крушение старого взгляда на аксиомы привело к раздвоению самого понятия «аксиома». Всё возрастающая в связи с запросами практики необходимость экспериментировать в области построения новых теорий, заменять одну аксиому другой, а так же их относительность, зависимость от ранее встречавшихся конкретных условий опыта и уровня науки, приводящая к невозможности выбрать раз и навсегда в качестве аксиомы такие положения, которые будут истинны абсолютно во всех условиях – всё это обусловило появление понятия аксиомы, несколько отличного от традиционного. Понятие аксиомы в этом смысле зависит от того, построение какой теории рассматривается и как оно проводится. Аксиомами данной теории называются просто те предложения этой теории, которые при данном построении её как дедуктивной принимаются за исходные, притом совершенно независимо от степени их простоты и очевидности.

Заключение