III, 5. Пусть А, В и С – три точки, не лежащие на одной прямой, А’, B’ и С’ – другие три точки, также не лежащие на одной прямой. Тогда если отрезок АВ конгруэнтен отрезку А’B’, отрезок АС конгруэнтен отрезку А’C’ и конгруэнтен , то конгруэнтен и конгруэнтен

Договоримся теперь о сравнении неконгруэнтных отрезков и углов.

Будем говорить, что отрезок АВ больше отрезка А’B’, если на прямой, определяемой точками А и В, найдётся лежащая между этими точками точка С такая, что отрезок АС конгруэнтен отрезку А’В’. Будем говорить, что отрезок АВ меньше отрезка А’B’, если отрезок А’B’ больше отрезка АВ.

Символически тот факт, что отрезок АВ меньше отрезка А’B’ (конгруэнтен отрезку А’B’) будем записывать так:

АВ<A’B’ (AB=A’B’).

Будем говорить, что больше , если в плоскости, определяемой , найдётся луч ОС, все точки которого являются внутренними точками , такой, что конгруэнтен . Будем говорить, что меньше , если больше .

С помощью аксиом принадлежности, порядка и конгруэнтности можно доказать целый ряд теорем элементарной геометрии. Сюда относятся: 1) три широко известные теоремы о конгруэнтности (равенстве) двух треугольников, 2) теорема о конгруэнтности вертикальных углов, 3) теорема о конгруэнтности всех прямых углов, 4) теорема о единственности перпендикуляра, опущенного из точки на прямую, 5) теорема о единственности перпендикуляра, проведённого к данной точке прямой, 6) теорема о внешнем угле треугольника, 7) теорема о сравнении перпендикуляра и наклонной.

IV. Аксиомы непрерывности

С помощью аксиом принадлежности, порядка и конгруэнтности мы произвели сравнение отрезков, позволяющее заключить, каким из трёх знаков <, = или > связаны эти отрезки.

Указанных аксиом, однако, недостаточно 1) для обоснования возможности измерения отрезков, позволяющее поставить в соответствие каждому отрезку определённое вещественное число, 2) для обоснования того, что указанное соответствие является взаимно однозначным.

Для проведения такого обоснования следует присоединить к аксиомам I, II и III две аксиомы непрерывности.

IV, 1 (аксиома Архимеда). Пусть АВ и СD – произвольные отрезки. Тогда на прямой, определяемой точками А и В существует конечное число точек А1, А2, ., Аn, расположенных так, что точка А1 лежит между А и А2, точка А2 лежит между А1 и А3, ., точка Аn-1 лежит между Аn-2 и Аn, причём отрезки АА1, А1А2, ., Аn-1An конгруэнтны отрезку CD и точка В лежит между А и Аn.

IV, 2 (аксиома линейной полноты). Совокупность всех точек произвольной прямой а нельзя пополнить новыми объектами (точками) так, чтобы 1) на пополненной прямой были определены соотношения «лежит между» и «конгруэнтен», определён порядок следования точек и справедливы аксиомы конгруэнтности III, 1 – 3 и аксиома Архимеда IV, 1, 2) по отношению к прежним точкам прямой определённые на пополненной прямой соотношения «лежит между» и «конгруэнтен» сохраняли старый смысл.

Присоединение к аксиомам I, 1 – 3, II и III, 1- 3 аксиомы Архимеда позволяет поставить в соответствие каждой точке произвольной прямой а определённое вещественное число х, называемое координатой этой точки, а присоединение ещё и аксиомы линейной полноты позволяет утверждать, что координаты всех точек прямой а исчерпывают множество всех вещественных чисел. Пользуясь этим, можно обосновать метод координат.

V. Аксиома параллельности

Самая последняя аксиома играет в геометрии особую роль, определяя разделение геометрии на две логически непротиворечивые и взаимно исключающие друг друга системы: евклидову и неевклидову геометрии.

В геометрии Евклида эта аксиома формулируется так.

V. Пусть а – произвольная прямая и А – точка, лежащая вне прямой а, тогда в плоскости α, определяемой точкой А и прямой а существует не более одной прямой, проходящей через А и не пересекающей а.

Долгое время геометры пытались выяснить, не является ли аксиома параллельности следствием всех остальных аксиом. Этот вопрос был решен Николаем Ивановичем Лобачевским, который доказал независимость аксиомы V от аксиом I – IV.

По-другому результат Лобачевского можно сформулировать так: если к аксиомам I – IV присоединить утверждение, отрицающее справедливость аксиомы V, то следствия всех этих положений будут составлять логически непротиворечивую систему (неевклидову геометрию Лобачевского).

Систему следствий, вытекающих из одних только аксиом I – IV обычно называют абсолютной геометрией. Абсолютная геометрия является общей частью как евклидовой, так и неевклидовой геометрий, ибо все предложения, которые могут быть доказаны только с помощью аксиом I – IV, верны как в геометрии Евклида, так и в геометрии Лобачевского.

Доказательство непротиворечивости аксиоматики Гильберта

Чтобы доказать непротиворечивость некоей теории Х, необходимо из материала другой, заведомо непротиворечивой, теории А построить такую модель, в которой выполняются все аксиомы теории Х. Если это удастся, теорию Х можно считать непротиворечивой. Следовательно, для того, чтобы доказать непротиворечивость гильбертовой системы, необходимо построить такую модель евклидовой геометрии, в которой выполнялись бы все аксиомы, предложенные Гильбертом.

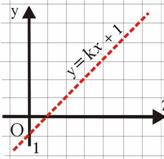
Для построения такой модели, необходима вышеупомянутая заведомо непротиворечивая теория. В модели, построенной Гильбертом, такой теорией служит теория действительных чисел. Идея построения модели состояла в рассмотрении системы координат на плоскости. В такой системе каждой точке М плоскости соответствуют два числа х и у – её координаты (рис. 3). Чтобы понять суть построения модели забудем о плоскости и имеющейся на ней координатной системе, «точками» будем называть упорядоченные пары действительных чисел (х; у) т. е. пары (х; у) и (у; х) с различными х и у будем считать различными. Теперь попытаемся определить «прямую». Вспомним, что каждая прямая описывается в координатах линейным уравнением вида ax + by + c = 0, где хотя бы один из коэффициентов a и b отличен от нуля. Например, уравнение прямой, не параллельной оси ординат, имеет вид у = kx + l, или, что то же самое, ax + by + c = 0, где a = k, b = -1, c = l (рис.4). Если же прямая параллельна оси ординат, ей соответствует уравнение x = p (т. е. уравнение ax + by + c = 0, где a = 1, b = 0, c = -p; рис. 5). При этом если все коэффициенты уравнения ax + by + c = 0 умножить на одно и то же число k ≠ 0, то полученное уравнение будет описывать ту же прямую. Мы же в своей модели будем называть «прямой» любое линейное уравнение вида ax + by + c = 0, в котором хотя бы один из коэффициентов a и b отличен от нуля, причём коэффициенты рассматриваются с точностью до ненулевого множителя пропорциональности (при k ≠ 0 уравнения ax + by + c = 0 и (ak)x + (bk)y + kc = 0 считаются одной и той же прямой).