2. Исследование внутривидового генетического разнообразия требует комплексного подхода, принимая во внимание комплексность механизмов, которые определяют внутривидовую изменчивость и дифференциацию.

3. Модели популяционно-генетической организации вида

Модель панмиктической популяции.

Простейший тип популяционной структуры представляет модель панмиктической популяции. Параметрами этой модели являются p и Ne. В начале любого популяционного исследования именно эту модель, с отсутствием какой либо генетической дифференциации (гетерогенности) и равновесием Х-В, необходимо тестировать в первую очередь. В том виде, как она сформулирована для случая множественных аллелей, эта модель такова: (Σ pkAij)2 = Σ p2kAiAi + Σ 2pk(1-pk) AiAj, где Aij обозначает аллель i или j, pk его частоту, k = 1,2,3 j – порядковые номера аллелей и Σpk = 1.

Модели подразделенной популяции.

Островная модель.

Имеются два варианта этой модели. Схема одного из них дана выше. Во втором варианте «острова архипелага» равны в размере и обмениваются друг с другом m иммигрантами с равной вероятностью, а «континент» не рассматривается. Генофонд мигрантов формируется совместным вкладом из всех субпопуляций. Расстояния между субпопуляциями не влияют на поток генов. По генетическим последствиям эти два варианта подразделенной популяции идентичны.

Для простоты, можно не принимать в расчет возможное действие естественного отбора. То есть, рассмотреть действие только параметров p, Ne и m. В этом случае только дрейф генов будет определять дифференциацию субпопуляций, а равновесное состояние частот аллелей будет достигаться при влиянии потока генов (миграции). Дифференциация задается выражением (1).

σ2δ’’ = p (1 - p) Fst(t), (1)

где Fst(t) = (1 - m)2[1/2N+(1-1/2N) Fst(t-1)]. (2)

Если выразить в (2) F через m и наоборот, то можно получить хорошо известные равенства (Ли, 1978, p. 474):

(1 - m)2 = 2N Fst / ((2N - 1) Fst + 1), (3)

Fst = (1 - m)2 / (2N - (2N - 1)(1 - m)2). (4)

Эти соотношения свидетельствуют об отрицательной связи между дрейфом и миграцией в межгрупповой дифференциации, которая определяется величиной Ne и значением коэффициента миграции. При небольшой интенсивности миграции (m << 1) из (4) и (1) можно вывести более простое выражение для генетической дисперсии или дифференциации (Wright, 1931; Колмогоров, 1935):

σ2δ’ = p (1 - p) / (4Nm + 1). (5)

Из последнего соотношения теперь ясно, почему Fst = 1 / (4Nm + 1), как было дано в предыдущей лекции. Здесь важно отметить, что для каждого текущего поколения важным является не само по себе действие m или Ne, но их произведение Nm; то есть, ключевым является совокупный эффект в виде числа мигрантов (причем речь идет о потоке генов, или иначе, о мигрантах, которые оставляют потомство!).

При взаимодействии дрейфа (изменения Ne) и миграции изменение частоты аллеля во времени - это комплексная функция распределения плотности вероятности (Wright, 1938; 1969). Объяснение этого выражения находится вне задач этого курса. Соотношение между Nm и Fst в состоянии стационарности, при равновесии дрейфа и миграции, показано графически (Рис. 18).

Модель ступенчатой миграции.

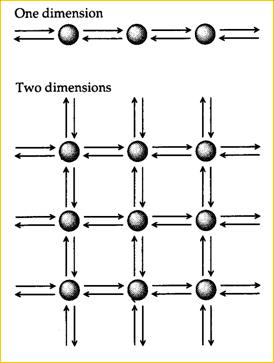
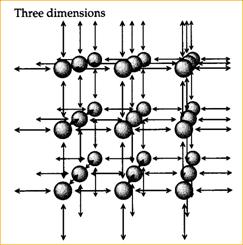
Одно-, двух- и трехмерные модели ступенчатой миграции были разработаны Кимурой с коллегами (Kimura, 1953; Kimura, Weiss, 1964; Weiss, Kimura, 1965). Мы не будем рассматривать детали этих моделей. Однако некоторое схематическое представление о них, мы предлагаем (Рис. 19). По меньшей мере, исходя из одномерной модели, даже интуитивно очевидно, что для этого случая между миграцией и генетическим расстоянием (генетической дифференциацией) существует обратно пропорциональная зависимость.

	Рис. 19. Характер миграции при одно-, двух- и трехмерной моделях ступенчатой миграции. Каждая стрелка представляет темп миграции m/2 в одном измерении, m/4 в двух измерениях и m/6 в каждом направлении в трех измерениях. Краевые эффекты могут быть элиминированы превращением одномерного массива в круг, двумерного массива – в поверхность сферы, а трехмерного массива – в тор (По Hartl, Clark, 1989).
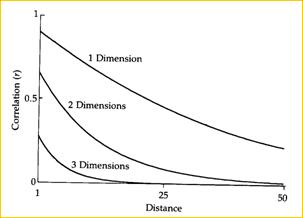
		В теории подразделенной популяции (последний вариант) имеется ясное предсказание взаимосвязи между степенью генетической дифференциации и расстояниями между субпопуляциями или демами (Рис 20), которое подтверждается эмпирическими исследованиями (Рис. 21). Также, сохраняется верным общее равновесное соотношение для случая нейтральности (модель без отбора): Fst = 1 / [4Nm + 1]. Рис 20. Уменьшение корреляции частоты аллеля с расстоянием для одно-, двух- и трехмерных моделей ступенчатой миграции (По Kimura, Weiss, 1964).
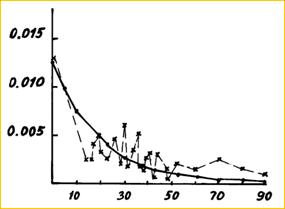
d φ Expected Empirical		Рис 21. Связь между географическим расстоянием (d, км) и генетической близостью между ними (φ) (По Workman et al., 1973 с добавлениями). φ(d) = a*e - bd, где a – коэффициент локального сходства, b – функция широкомасштабной миграции.