Главные факторы популяционно-генетической динамики.

Среди факторов, влияющих на динамику, имеются случайные, или стохастические, и систематические. Например, случайный дрейф генов – это один из наиболее важных стохастических факторов генетической дифференциации, особенно в малых популяциях. Естественный отбор и миграция – это систематические факторы. Основные популяционно-генетические параметры, которые определяют степень генетической дифференциации, это: (1) p – частота аллеля , (2) Ne – генетически эффективная (или просто эффективная) численность популяции, (3) m – коэффициент миграции, (4) s – коэффициент естественного отбора.

Можно проиллюстрировать действие факторов, начав с первого и второго параметров. Для начала, рассмотрим дрейф генов во времени для одной популяции небольшого размера. Дрейф генов возникает как результат стохастических ошибок при передаче генов из одного поколения в следующее поколение. Пусть численность популяции и частота аллеля (скажем, А) в ней равны Ne = N = 10 и pA = 0.5, в исходном поколении (t0). В этом случае можно рассчитать стандартную ошибку: SE = Ö[(0.5*0.5)/20] = 0.16. То есть, в следующем поколении pA должна быть 0.5 ± SE. Другими словами, некоторые из выборок генофонда, дающие следующее поколение, могут иметь частоты: pA = 0.7 или pA = 0.3 (33% вероятности), или даже 0.5 ± 2SE, pA = 0.9 или pA = 0.1 (5% вероятности), с некоторыми упрощениями для большей ясности. Очевидно, что очень скоро в такой маленькой популяции десяти особей (N = 10) определенный аллель будет либо фиксирован (pA = 1), либо утерян (pA = 0). Все сделанные заключения остаются верными для случаев, когда дрейф происходит в пространстве (Wright, 1943, Li, 1955).

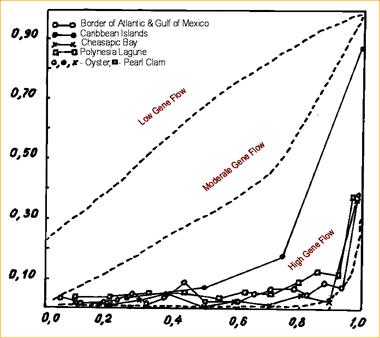
Миграция и естественный отбор – это два следующих, из четырех важнейших факторов, влияющих на популяционную структуру. Мы рассмотрим подробнее влияние этих двух факторов в следующей лекции. Миграция влияет не только на интегрированность генофонда, но и на эффективную численность популяций, объединяя их (Рис. 4). Данные на Рис. 4 для морских беспозвоночных соответствуют высоким значениям миграции или потока генов. Аналитически m (коэффициент миграции) и Ne связаны пропорциональной зависимостью.

Влияние естественного отбора многогранно. Практически все процессы в популяции отбор может усиливать или тормозить. Влияние дрейфа генов при действии стабилизирующего отбора уменьшается, а при направленном отборе фиксация частоты происходит с ускоренной скоростью. Имеется множество разработанных моделей действия тех или иных факторов отбора.

Мера межпопуляционной дифференциации

В качестве меры степени генетической дифференциации между популяциями, или наоборот внутри них, полезными являются статистики Fst и Dm, первая – это стандартизированная дисперсия частот аллелей, а вторая – минимальное генетическое расстояние. Использование Fst (или Gst) при популяционном анализе является более предпочтительным вместе с некоторыми деталями свойств статистик. Простейший способ понять, что такое Fst – это определить данную меру дифференциации в терминах гетерозиготности (разнообразия), как нормированную гетерозиготность: Fst = (Ht - Hs) / Ht. Здесь Hs – это ожидаемая гетерозиготность в субпопуляции (или внутри выборки), а Ht – это ожидаемая гетерозиготность во всей популяции (или в совокупности выборок). В этом определении Fst = Gst (Nei, 1977b).

Простейшая модель популяционной структуры.

Соотношение Харди-Вайнберга: (p + q)2 = p2 + 2pq + q2. Это равновесная модель для большой (бесконечной в теории) популяции случайно скрещивающихся двуполых особей. Она объясняет стабильность частот аллелей и в меньшей степени частот генотипов при отсутствии давления систематических факторов, основными из которых, в текущем поколении являются естественный отбор и миграция.

Комплексная природа генетической динамики и стационарности.

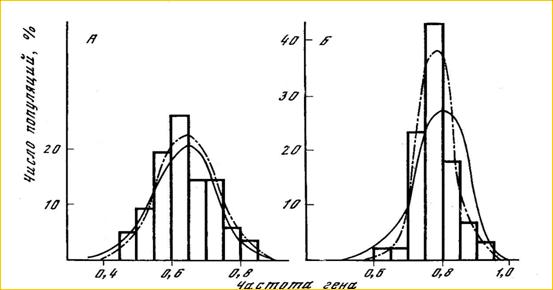
В природе ни один из перечисленных факторов не действует по отдельности. Обычно они взаимодействуют в различных комбинациях и варьируют сами в пространстве, в различных частях ареала, и во времени, в поколениях, от молодых когорт - к взрослым, или в онтогенезе, и даже в пределах той же самой когорты в течение сезонов года. Классическим примером изменчивости в природной популяции (ни кто еще не повторил с середины 70-х голов) является полиморфизм двух аллозимных локусов нерки, который подвержен влиянию двух факторов (Рис. 5). По локусу PGM* кривая, построенная с учетом некоторого давления отбора вместе с миграцией и вариацией

Частота аллеля PGM* LDH*

Рис. 5. Распределение частот аллелей по локусам LDH* и PGM* в нерестовых скоплениях нерки (O. nerka) в озере Азабачье (Камчатка) (По Алтухов и др., 1975). Гистограмма показывает фактическое распределение частот. Пунктирной линией показаны частоты, ожидаемые согласно островной модели Райта при действии дрейфа, миграции и естественного отбора, определяемых тремя параметрами – Ne, m, и s. Непрерывной линией показана вариация, зависимая только от Ne и m (дрейф и миграция). LDH*