Антагонистические игрыРефераты >> Менеджмент >> Антагонистические игры
(16)
являются k-м приближением к оптимальным стратегиям игроков. При этом
![]()
является приближением к положению равновесия (седловой точке), так как седловая точка находится между vmaxk и vmink. Точность этого приближения можно оценить соотношением
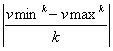
Итерационный процесс сходится, т. е. после достаточного числа итераций можно получить решение с заданной точностью. Но у данного метода довольно малая скорость сходимости, т. е. для получения приемлемого решения необходимо выполнить большое число итераций.
Задачи
Принятие решений при совместных действиях.
1. задача
Магазин может завести в различных пропорциях товары типа (А, Б, В). Их реализация, а следовательно и прибыль (Сij) завися от вида товара и состояния спроса. Предполагая, что последний может характеризоваться тремя состояниями (1 2 3) и учитывая, что спрос зависит от моды и прогнозировать его невозможно, определить оптимальные пропорции в закупке товаров из условия гарантированной прибыли при следующих вариантах матриц.
1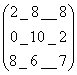 2
2
вариант 1
При сведении этой задачи к задаче линейного программирования получаем результат
Седловая точка: 6,6
Оптимальная стратегия первого игрока:
x1 = 0,1
x2 = 0,1
x3 = 0,8
Оптимальная стратегия второго игрока:
y1 = 0,2
y2 = 0,6
y3 = 0,1
Это означает, оптимальные пропорции выпуска товаров являются:
10% доля товара А, 10% доля товара Б, 80% доля товара В.
При этом соотношении магазин получит доход не менее 6,6.
вариант 2
Седловая точка: 13,8
Оптимальная стратегия первого игрока:
x1 = 0
x2 = 0,8
x3 = 0,2
Оптимальная стратегия второго игрока:
y1 = 0,1
y2 = 0,9
y3 = 0
При данных матрицы 2 разумнее всего 80% продавать товара Б и 20% товара В, при этом товар А вообще не реализуется. Магазин получит доход не менее 13,8
Задача 2
Магазин может завести в различных пропорциях товары типа (А, Б, В). Их реализация, а следовательно и прибыль (Сij) завися от вида товара и состояния спроса. Предполагая, что последний может характеризоваться тремя состояниями (1 2 3) и учитывая, что спрос зависит от моды и прогнозировать его невозможно, определить оптимальные пропорции в закупке товаров из условия гарантированной прибыли при следующей матрице.

Точность: 0,5
Седловая точка: 14,8
Оптимальная стратегия первого игрока:
x1 = 0,3
x2 = 0
x3 = 0,7
Оптимальная стратегия второго игрока:
y1 = 0,1
y2 = 0
y3 = 0,9
Методом Брауна-Робинсона установлено, что наилучший вариант реализации продукции для магазина 30% товара А, 70% товара В. При этом гарантирован доход 14,8.
Задача 3
Является ли игра с платежной матрицей
| (60, 20) | (10, 50) | (20, 80) |
| (40, 70) | (40, 20) | (50, 30) |
| (80, 50) | (30, 60) | (90, 70) |
Антагонистической?
Существуют ли в ней
1. ситуация равновесия в чистых стратегиях?
2. Вполне смешанная ситуация?
3. Ситуация оптимальная по Парето?
Чтобы назвать эту игру антагонистической нужно, чтобы выполнялось условие:
aij + bij = 0 или aij + bij = const , в данном случае игра не является антагонистической.
1. В игре не существует ситуация равновесия в чистых стратегиях.
2. В игре не существует вполне смешанной ситуации.
3. Расчет игровых ситуаций оптимальных по Паретто
Платежная матрица игрока 1
60 10 20
40 40 50
80 30 90
Платежная матрица игрока 2
20 50 80
70 20 30
50 60 70
Множество ситуаций, оптимальных по Парето, содержит 2 элемента: (1, 3) (3, 3)
