В игре, моделирующей кредитование проектов, 2-й столбец доминирует 1-й, а 4-й доминирует 3-й, т. е. игрок 2 не будет ис­кать свои 1-ю и 3-ю чистые стратегии, поэтому их можно сматривать. Упрощённая платёжная матрица игры:

Для полного анализа игры достаточно рассмотреть эти матрицы.

Другой способ упрощения платёжной матрицы — преобразование её элементов. Пусть каждый элемент платёжной матрицы изменяется по правилу (k ≠ 0). Тогда оптимальные стратегии игр с платёжными матрицами и сопадают, а седловая точка игры равна .

Выполнив преобразование, можно упростить платежиvi матрицу и последующий анализ. Кроме того, из этого свойства следует, что можно изменять масштаб элементов матрицы, то есть менять единицы, в которых задаётся выигрыш.

Упрощение платёжной матрицы важно, если анализ игры выполняется вручную или графическим методом. Если же для нахождения оптимальных стратегий используются численные методы, например итерационные, то усилия и время, затрачиваемые на поиск доминируемых стратегий и подходящего преобразования элементов платёжной матрицы, могут оказаться потраченными зря, поскольку численный анализ исходной и упрощенной матриц выполняется по одному и тому же алгоритму, а разница во времени вычислений несущественна для человека, однако существуют платёжные матрицы, численный анализ которых до упрощения сложен.

Один из способов нахождения оптимальной стратегии игроков — сведение матричной игры к задаче линейного программирования.

Игрок 1 рассматривает минимальные ожидаемые выигрыши, при этом он ищет свою оптимальную стратегию ξ и седловую точку (число v), такие что

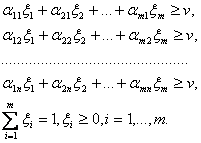
аналогично игрок 2 минимизирует платежи, то есть ищет вектор η=(η1,η2,…,ηn) и седловую точку v, такие что выполнялись те же неравенства.

Будем считать, что выполнены преобразования, в результате которых получена платёжная матрица А, все элементы которой положительны. Тогда можно считать число v также поло­чным: v>0. Разделим соотношения (7) на v и определим:

Задача игрока 1 — максимизировать выигрыш, т.е. максимизировать v. Поскольку

(9)

то v максимально, когда минимальна.

Аналогично, задача игрока 2- минимизировать v, а так как

(10)

то v минимальна, когда максимальна.

Тогда анализ платёжной матрицы с точки зрения игрока 1 эквивалентен задаче линейного программирования: найти минимум целевой функции.

f = x1+x2+…+xm

при условиях

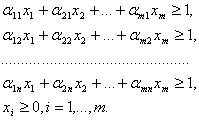
(11)

Задачу игрока 2 также можно сформулировать как задачу линейного программирования, двойственную к задаче (11): найти максимум целевой функции

g = y1+y2+…+yn

при условиях

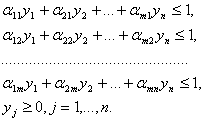
(12)

Задачи линейного программирования (11) и (12) можно решить, например, симплекс-методом.

Пусть у* = (у*1, у*2, ., у*n)- решение задачи линейного программирования (12), х* = (х*1, х*2, ., х*­m) — теневые цены (решение двойственной задачи). Тогда значение седловой точки v определяется из условий (9), (10):

(13)

а оптимальные стратегии игроков получаются из решения з| чи линейного программирования нормированием:

ξ*i=v x*i ,i=1,…,m,

η*j=v y*j ji=1,…,n. (14)

Пусть антагонистическая игра задана платёжной матрицей . Словесно-формульное описание алгоритма анализа платёжной матрицы антагонистической игры сведением к задаче линейного программирования:

1* начало процесса.

2* ввод платёжной матрицы игры А.

3* Формулировка задачи линейного программирования (12): найти максимум функции

при условиях Ay ≤ 1, y≥ 0.

4* Решение задачи линейного программирования (12). Результат

у* = (у*1, у*2, ., у*n)- оптимальный вектор, х* = (х*1, х*2, ., х*­m) теневые цены.

5* Определение положения равновесия: ;

оптимальной стратегии игрока 1:

оптимальной стратегии игрока 2:.

6* Вывод результата

7* Конец процесса

Другой способ нахождения оптимальных стратегий игроков и седловой точки игры — решать матричную игру с помощью итерационных методов.

Рассмотрим простейший итерационный метод нахождения оптимальных стратегий в матричных играх - метод Брауна-Робинсона. Идея метода состоит в следующем: имитируется многократное повторение игры и набирается статистика, показывающая какие стратегии максимизируют выигрыш, и таким образом определяется оптимальная стратегия.

Для анализа антагонистической игры с матрицей

строится итерационный процесс, каждый шаг которого - розыгрыш игры. В первой игре у игроков ещё нет никакой информации, поэтому они выбирают свои стратегии произвольно. Положим для определённости, что в первой игре оба игрока всегда выбирают свои 1-е чистые стратегии:

k =1 ; ξ1 = (1,0,…,0); η1=(1,0,…,0).

Верхний индекс обозначает номер игры k. Предположим, состоялось k игр, в них игрок 1 использовал свою i-ю стратегию ξki раз, а игрок 2 использовал свою j-ю стратегию ηkj раз. Определим максимальный ожидаемый выигрыш игрока 1 и минимальный ожидаемый проигрыш игрока 2 с учётом результатов состоявшихся игр:

(15)

В (k + 1)-й игре игрок 1 должен использовать свою стратегию ik+1 , доставляющую максимальный ожидаемый выигрыш vmaxk, а игрок 2 – стратегию jk+1, обеспечивающую минимальный ожидаемый проигрыш vmink. Тогда векторы, координаты которых равны частотам, с которыми чистые стратегии обеспечивали максимальный выигрыш игроку 1 и минимальный проигрыш игроку 2