Поскольку суммарный сбыт предприятий в каждом случае полностью обеспечивает рынок (сумма чисел в каждой ячейке таблице равна 1000), то интересы предприятий противоположны, и данную ситуацию можно смоделировать в виде антагонистической игры. Первое предприятие является игроком 1, и у него есть четыре стратегии: выпускать продукцию А1, а2 а3 и A4. Его противник (2-е предприятие) имеет три стратегии: выпускать продукцию В1, В2 и B3. Каждое из предприятий намерено выбрать стратегию, гарантирующую максимальную прибыль при любых действиях противника.

В таблице 1 представлена платёжная матрица этой игры. На пересечении i-й строки и J-го столбца матрицы находится число aij — выигрыш 1-го игрока, если он выпускает продукцию Ai, а его противник — Bi. Выигрыш 2-го игрока при этом равен 1000 — aij (таким образом, это — антагонистическая игра с постоянной суммой):

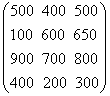Рассмотрим другую ситуацию. Пусть некоторый банк может принять участие в кредитовании трёх проектов. Возврат кредита и получение дохода зависят от общей финансовой ситуации, которая сложится в будущем году. Существующие прогнозы будущей финансовой ситуации противо­речивы. Специалисты банка составили классификацию возможных финансовых ситуаций и сделали прогноз эффективности кредитования (табл. 2). Так, если сложится исключительно благоприятная финансовая ситуация, то кредитование 1-го проекта обещает прибыль 720 денежных единиц, 2-го – 660, а 3-го – 440.

Таблица 2

Банк хочет спланировать кредиты, чтобы гарантировать наибольший доход даже при наиболее неблагоприятной финан­совой ситуации. Данную ситуацию можно смоделировать в виде антагонистической игры. Банк является игроком 1, он имеет три стратегии: кредитовать проект 1, 2 или 3. Его противник — при­рода (общая финансовая ситуация) является игроком 2. Будем считать, что у игрока 2 имеется пять стратегий: исключительно благоприятная общая финансовая ситуация, благоприятная, нейтральная, неблагоприятная и исключительно неблагоприят­ная. Поскольку банк хочет получить максимальный доход при самой неблагоприятной ситуации, то предполагаем, что природа «хочет» навредить банку как можно сильнее. Если ситуация бу­дет лучше, то доход банка увеличится. В табл. 2 представлена платёжная матрица этой игры:

Рассмотрим платёжную матрицу произвольной антагони­стической игры. Основное предположение при ана­лизе антагонистических игр: каждый игрок действует наилуч­шим для себя образом, т. е. пытается получить максимально возможный выигрыш при любых стратегиях противника, считая, что противник также действует наилучшим для себя образом. Следовательно, игрок 1 считает, что при выборе им любой стра­тегии (любой строки платёжной матрицы), противник выберет столбец, дающий ему максимальный выигрыш, т. е. минималь­ный для игрока 1. Тогда оптимальная стратегия игрока 1 - вы­брать самый большой из минимальных выигрышей, т. е. выбрать

v = max min aij (2)

i j

Эта стратегия гарантирует наибольший выигрыш незави­симо от стратегии противника. Такая стратегия называется максиминной стратегией (стратегия максимизации минимального выигрыша), а v — максимином.

Аналогично, если игрок 2 выбирает j-ю стратегию, то в худшем случае он проигрывает max aij

i

поэтому его гарантированный проигрыш:

v*= min max aij

j i (3)

Такая стратегия называется минимаксной стратегией (стратегия минимизации максимального проигрыша), а v- минимаксом.

Например, в игре, моделирующей конкуренцию предпри­ятий, игрок 1 считает, что независимо от его стратегии выбора продукции для производства (т. е. независимо от выбора им строки платёжной матрицы), игрок 2 выберет стратегию (столбец платёжной матрицы), максимизирующую его выигрыш, т.е. минимизирующую выигрыш игрока 1. Если игрок 1 будет произво­дить продукцию А1 (выберет 1-ю строку платёжной матрицы), то игрок 2 может производить продукцию В2 (выбрать 2-й столбец), тогда выигрыш игрока 1 равен 400, а выигрыш игрока 2 — 600. Если игрок 1 будет производить продукцию А2 (выберет 2-ю строку), то игрок 2 может производить продукцию В1 (выбрать 1-й столбец). Тогда выигрыш игрока 1 будет 100, а игрока 2 - 900. Поэтому игроку 1 нужно найти минимальный выигрыш в каждой строке платёжной матрицы и рассматривать только его. Этот выигрыш ему гарантирован. Рассмотрим платёжную матрицу этой игры:

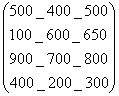Справа в столбец выписаны минимальные элементы каждой строки. Оптимальная стратегия игрока 1- выбрать строку с самым большим минимальным элементом, это гарантируем ему наибольший выигрыш, независимо от стратегии игрока 2. Максимальный среди минимальных элементов строк выигрыш 700 (он заключён в квадрат). Следовательно, при выпуске любой продукции 2-м предприятием, доход 1-го предприятия не будет меньше 700 денежных единиц, если он будет выпускать продукцию А3. Таким образом, для игрока 1 максиминной является 3-я стратегия, она оптимальна. Максимин равен: