Задачу выбора масштабного коэффициента КA усложняет необходимость сохранять соответствие разрядов всех чисел, которыми оперирует цифровой автомат. Пусть имеется цифровой автомат с разрядной сеткой длиной 12 двоичных разрядов (рис. 2, а). Надо определить масштабный коэффициент для чисел A1 = - 1011,01111102 и A2 = 0,1100011012.

Для того чтобы выполнить условие (19), необходимо число, большее по абсолютному значению, записать в виде А1 = -0,10110111110 · 24. Отсюда [A1]ф = 1,10110111110, что соответствует величине масштабного коэффициента = 24. Число А2 должно войти в разрядную сетку автомата с сохранением соответствия разрядов, т. е.. Следовательно, А2 = +0,0000110001101·24 или [А2]ф = 0,00001100011 (рис. 2, б, в).

Из примера видно, что представление чисел в форме с фиксированной запятой может привести к погрешности представления. Так, для числа А2 абсолютная погрешность представления оценивается величиной части числа, не уместившейся в разрядную сетку, т. е. величиной 0,0000000000001·24. В некоторых случаях очень малые числа представляются в машине изображением, называемым машинным нулем. Следовательно, ошибка представления зависит от правильности выбора масштабных коэффициентов. Вычисление последних должно проводиться таким образом, чтобы исключить возможность появления в процессе функционирования автомата чисел, машинные изображения которых не удовлетворяют условию (19). Если в результате операции появится число, по абсолютному значению большее единицы, то возникает переполнение разрядной сетки автомата, что нарушает нормальное функционирование цифрового автомата.

Представление чисел в форме с плавающей запятой. В нормальной форме

(20)

где тA —мантисса числа А; рA —порядок числа А.

Как видно из ранее изложенного, такое представление чисел не однозначно; для определенности обычно вводят некоторые ограничения. Наиболее распространено и удобно для представления в ЭВМ ограничение вида

, (21)

где q — основание системы счисления.

Нормализованная форма представления чисел — форма представления чисел, для которой справедливо условие (21).

Поскольку в этом случае абсолютное значение мантиссы лежит в пределах от q-1 до 1 – q-n, где п — количество разрядов для изображения мантиссы без знака, положение разрядов числа в его автоматном изображении не постоянно. Поэтому такую форму представления чисел называют также формой представления с плавающей запятой. Формат машинного изображения числа с плавающей запятой должен содержать знаковые части и поля для мантиссы и порядка (рис. 3, а). Выделяются специальные разряды для изображения знака числа (мантиссы) и знака порядка или характеристики (рис. 3, а, б). Кодирование знаков остается таким же, как было с фиксированной запятой.

Рассмотрим пример записи чисел в форме с плавающей запятой. Пусть в разрядную сетку цифрового автомата (рис. 3) необходимо записать двоичные числа A1 = -10110,11112 и А2 = +0,0001100101112.

Прежде всего эти числа необходимо записать в нормальной форме (рис. 3, в, г). Порядок чисел выбирают таким образом, чтобы для них выполнялось условие (21), т. е. A1 = -0,101101111·25 и А2 = +0,110010111·2-3, он должен быть записан в двоичной системе счисления. Так как система счисления для заданного автомата остается постоянной, то нет необходимости указывать ее основание, достаточно лишь представить показатель степени.

Рис. 3. Представление чисел в форме с плавающей запятой

Поскольку для изображения порядка выделено пять цифровых разрядов и один разряд для знака, их машинные изображения и машинные изображения их мантисс соответственно

[] = 000101; [].= 00011;

[] = 1,101101111; [] = 0,110010111.

1.3 Погрешности представления числовой информации

Представление числовой информации в цифровом автомате, как правило, влечет за собой появление погрешностей (ошибок), величина которых зависит от формы представления чисел и от длины разрядной сетки автомата.

Абсолютная погрешность представления — разность между истинным значением входной величины А и ее значением, полученным из машинного изображения Ам, т. е. Δ[А] = А – Ам.

Относительная погрешность представления — величина

. (30)

Входные величины независимо от количества значащих цифр могут содержать грубые ошибки, возникающие из-за опечаток, ошибочных отсчетов показаний каких-либо приборов, некорректной постановки задачи или отсутствия более полной и точной информации. Например, часто принимают π = 3,14. Однако эта величина может быть получена с более высокой точностью. Если принять, что точное значение π = 3,14139265, то абсолютная погрешность равна Δ[π] = 0,00159265.

Часто некоторая величина в одной системе счисления имеет конечное значение, а в другой системе счисления становится бесконечной величиной, например, дробь 1/10 имеет конечное десятичное представление, но, будучи переведена в двоичную систему счисления, становится бесконечной дробью 0,00011000110011 . .

Следовательно, при переводе чисел из одной системы счисления в другую неизбежно возникают погрешности, оценить которые нетрудно, если известны истинные значения входных чисел.

В соответствии с (19) числа изображаются в машине в виде Аq = [А]КA, где масштабный коэффициент КA выбирают так, чтобы абсолютное значение машинного изображения числа А в системе счисления с основанием q = 2 было всегда меньше 1: Аq =КA [а-1q-1 + а-2q-2 + . + а-пq-n +…].

Так как длина разрядной сетки автомата равна п двоичных разрядов после запятой, абсолютная погрешность перевода десятичной информации в систему с основанием q будет

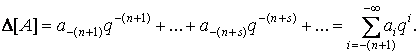(31)

Если q = 2 , то при аi = 1 максимальное значение этой погрешности

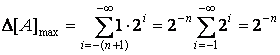(32)

Из (32) следует, что максимальная погрешность перевода десятичной информации в двоичную не будет превышать единицы младшего разряда разрядной сетки автомата. Минимальная погрешность перевода равна нулю.

Усредненная абсолютная погрешность перевода чисел в двоичную систему счисления Δ[A] = (0 + 2-n)/2 = 0,5·2-n.

Для представления чисел в форме с фиксированной запятой абсолютное значение машинного изображения числа