Представление числовой информации в информационных системахРефераты >> Информатика >> Представление числовой информации в информационных системах
Реферат
Курсовая работа: количество листов - , количество рисунков - 3, количество таблиц – 2, количество формул и уравнений – 36, количество программ – 1, источников – 18.
СИСТЕМА СЧИСЛЕНИЯ, ДЕСЯТИЧНАЯ, ДВОИЧНАЯ, ВОСЬМЕРИЧНАЯ, ШЕСНАДЦАТИРИЧНАЯ, ДРОБНАЯ, РАЗРАБОТКА ПРОГРАММЫ, РЕЗУЛЬТАТ ПРОГРАММЫ. ПОГРЕШНОСТИ
Результатом моего курсового проекта является разработанная мною программа, с помощью которой можно переводить из десятеричной системы счисления в восьмеричную (с использованием двоичной системы счисления) на языке Pascal, и изучение теоретического материала по теме «Представление числовой информации в информационных системах».
СОДЕРЖАНИЕ:
1. ПРЕДСТАВЛЕНИЕ ЧИСЛОВОЙ ИНФОРМАЦИИ В ИНФОРМАЦИОННЫХ СИСТЕМАХ
1.1 Перевод числовой информации из одной позиционной
системы в другую
1.2 Формы представления числовой информации
1.3 Погрешности представления числовой информации
2. Список используемой литературы
1. Представление числовой информации в информационных системах.
Выбор системы счисления для представления
числовой информации
Система счисления — совокупность приемов и правил для записи чисел цифровыми знаками или символами. Наиболее известна десятичная система счисления, в которой для записи чисел используются цифры 0, 1, ., 9. Способов записи чисел цифровыми знаками существует бесчисленное множество. Любая предназначенная для практического применения система счисления должна обеспечивать:
q возможность представления любого числа в рассматриваемом диапазоне величин;
q единственность представления (каждой комбинации символов должна соответствовать одна и только одна величина);
q простоту оперирования числами.
Все системы представления чисел делят на позиционные и непозиционные. Самый простой способ записи чисел может быть описан выражением
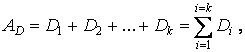
где AD — запись числа А в системе счисления D; Di — символы системы, образующие базу D = {D1, D2, ., Dk}.
По этому принципу построены непозиционные системы счисления.
Непозиционная система счисления — система, для которой значение символа не зависит от его положения в числе.
Принципы построения таких, систем не сложны. Для их образования используют в основном операции сложения и вычитания. Например, система с одним символом (палочкой) встречалась у многих народов. Для изображения какого-то числа в этой системе нужно записать количество палочек, равное данному числу. Эта система неэффективна, так как запись числа получается длинной. Другим примером непозиционной системы счисления является римская система, использующая набор следующих символов: I, X, V, L, С, D, М и т. д. В этой системе существует отклонение от правила независимости значения цифры от положения в числе. В числах LХ и ХL символ Х принимает два различных значения: +10 — в первом случае и -10 — во втором.
В общем случае системы счисления можно построить по следующему принципу:
![]() (1)
(1)
где АB — запись числа А в системе счисления с основанием Bi; аi — цифра (символ) системы счисления с основанием Bi; Bi — база, или основание системы.
Если предположить, что Bi = qi то с учетом (1)
Bi = qiBi-1 (2)
Позиционная система счисления — система, удовлетворяющая равенству (2).
Естественная позиционная система счисления имеет место, если q — целое положительное число.
В позиционной системе счисления значение цифры определяется ее положением в числе: один и тот же знак принимает различное значение. Например, в десятичном числе 222 первая цифра справа означает две единицы, соседняя с ней — два десятка, а левая — две сотни.
Любая позиционная система счисления характеризуется основанием. Основание (базис) q естественной позиционной системы счисления — количество знаков или символов, используемых для изображения числа в данной системе. Возможно бесчисленное множество позиционных систем, так как, приняв за основание любое число, можно образовать новую систему. Например, запись числа в шестнадцатеричной системе может проводиться с помощью следующих знаков (цифр): 0, 1, ., 9, А, В, С, D, Е, F (вместо А, ., F можно записать любые другие символы, например, ![]()
Для позиционной системы счисления справедливо равенство
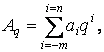 (3)
(3)
или ![]() где Aq—произвольное число, записанное в системе счисления с основанием q; п + 1, т — количество целых и дробных разрядов.
где Aq—произвольное число, записанное в системе счисления с основанием q; п + 1, т — количество целых и дробных разрядов.
На практике используют сокращенную запись чисел:
![]()
В восьмеричной системе счисления числа изображают с помощью цифр 0,1, .,7. Например, 124,5378 =1 82 + 2·81 + 4·80 + 5·8-1 + 3·8-2 + 7·8-3.
В двоичной системе счисления используют цифры 0, 1. Например, 1001,11012 = 1·23 + 0·22 + 0·21 + 1·20 + 1·2-1 + 1·2-2 + 0·2-3 + 1·2-4.
Для записи чисел в троичной системе берут цифры 0,1,2. Например,
21223 = 2·33 + 1·32 + 2·31 + 2·30.
В таблице 1 приведены эквиваленты десятичных цифр в различных системах счисления.
Таблица 3.1
| Десятичная цифра | Эквиваленты в других системах счисления | ||||
| q = 2 | q = 3 | q = 5 | q = 8 | q = 16 | |
| 0 | 0000 | 000 | 00 | 00 | 0 |
| 1 | 0001 | 001 | 01 | 01 | 1 |
| 2 | 0010 | 002 | 02 | 02 | 2 |
| 3 | 0011 | 010 | 03 | 03 | 3 |
| 4 | 0100 | 011 | 04 | 04 | 4 |
| 5 | 0101 | 012 | 10 | 05 | 5 |
| 6 | 0110 | 020 | 11 | 06 | 6 |
| 7 | 0111 | 021 | 12 | 07 | 7 |
| 8 | 1000 | 022 | 13 | 10 | 8 |
| 9 | 1001 | 100 | 14 | 11 | 9 |
| 10 | 1010 | 101 | 20 | 12 | A |
| 11 | 1011 | 102 | 21 | 13 | B |
| 12 | 1100 | 110 | 22 | 14 | C |
| 13 | 1101 | 111 | 23 | 15 | D |
| 14 | 1110 | 112 | 24 | 16 | E |
| 15 | 1111 | 120 | 30 | 17 | F |
