Для любой позиционной системы счисления справедливо, что основа­ние изображается символом 10 в своей системе, т. е. любое число можно записать в виде

(4)

В ЭВМ используют в основном позиционные системы счисления. В дальнейшем для простоты изложения будем употреблять термин «система счисления», имея в виду позиционные системы.

Вес разряда рi, числа в позиционной системе счисления выражается соотношением

(5)

где i — номер разряда при отсчете справа налево.

Если разряд имеет вес рi = 10k, то следующий старший разряд будет иметь вес рi+1 = 10k+1, а соседний младший разряд — вес рi-1 = 10k-1. Такая взаимосвязь разрядов приводит к необходимости передачи информации между ними.

Если в данном разряде накопилось значение единиц, равное или большее q, то должна происходить передача единицы в соседний старший разряд. При сложении такие передачи информации называют переносами, а при вычитании — заемами. Передача переносов или заемов происходит последовательно от разряда к разряду.

Длина числа (ДЧ) — количество позиций (или разрядов) в записи числа [14]. В техническом аспекте длина числа интерпретируется как длина разрядной сетки (ДРС).

Для разных систем счисления характерна разная длина разрядной сетки, необходимая для записи одного и того же числа. Например, 96 = 1208 = 101203 = 11000002. Здесь одно и то же число, записанное в разных базисах, имеет разную длину разрядной сетки. Чем меньше основание системы, тем больше длина числа.

Если длина разрядной сетки задана, то это ограничивает максимальное (или минимальное) по абсолютному значению число, которое может быть записано.

Пусть длина разрядной сетки равна любому положительному числу, например п. Тогда Аqmax = qn - 1; Аqmin = - (qn – 1).

Диапазон представления (ДП) чисел в заданной системе счисления — интервал числовой оси, заключенный между максимальным и минимальным числами, представленными длиной разрядной сетки:

Аqmax ≥ ДП ≥ Аqmin . (6)

Правильный выбор системы счисления — важный практический вопрос, поскольку от его решения зависят такие технические характеристики проектируемой ЭВМ, как скорость вычислений, объем памяти, сложность алгоритмов выполнения арифметических операций. При выборе системы счисления для ЭВМ необходимо учитывать следующее:

основание системы счисления определяет количество устойчивых состояний, которые должен иметь функциональный элемент, выбранный для изображения разрядов числа;

длина числа существенно зависит от основания системы счисления;

система счисления должна обеспечить простые алгоритмы выполнения арифметических и логических операций.

Десятичная система, столь привычная в повседневной жизни, не является наилучшей с точки зрения ее технической реализации в ЭВМ. Известные в настоящее время элементы, обладающие десятью устойчивыми состояниями (элементы на основе сегнетокерамики, декатроны и др.), имеют невысокую скорость переключения, а следовательно, не могут обеспечить соответствующее быстродействие машины.

Подавляющее большинство компонентов электронных схем, применяемых для построения ВМ, — двухпозиционные. С этой точки зрения для ЭВМ наиболее подходит двоичная система счисления. Но рационально ли использование этой системы с точки зрения затрат оборудования? Для ответа на этот вопрос введем показатель экономичности системы С — произведение основания системы на длину разрядной сетки, выбранную для записи чисел в этой системе:

С = qN, (7)

где q — основание системы счисления; N— количество разрядов.

Если принять, что каждый разряд числа представлен не одним элементом с q устойчивыми состояниями, а q элементами, каждый из которых имеет одно устойчивое состояние, то показатель экономичности укажет словное количество оборудования, которое необходимо затратить на представление чисел в этой системе.

Максимальное число, которое можно изобразить в системе с основанием q,

Аqmax = qN – 1.(8)

Из (8) можно найти требуемую длину разрядной сетки:

(9)

Тогда для любой системы счисления .

Представим, что величина q принимает любые значения (целочисленные и дробные), т. е. является непрерывной величиной. Это необходимо для того, чтобы рассматривать величину С как функцию от величины q. Данное допущение не является строгим, однако позволяет получить интересный вывод: если за единицу измерения оборудования принят условный элемент с одним устойчивым состоянием, то для сравнения двух систем счисления можно ввести относительный показатель экономичности

(10)

позволяющий сравнить любую систему счисления с двоичной.

Если функция F непрерывна, то, как видно из приведенного ниже соотношения, она имеет минимум.

q 2 3 4 6 8 10

F 1,000 0,946 1,000 1,148 1,333 1,505

На рис. 1 представлена зависимость величины F от основания системы счисления q. Нижняя точка графика соответствует минимуму функции F, определяемому из условия dF/dt = 0, что соответствует значению q = е. Следовательно, с точки зрения мини­мальных затрат условного оборудования, наиболее экономичной является система счисления с основанием, равным е ≈ 2,72.

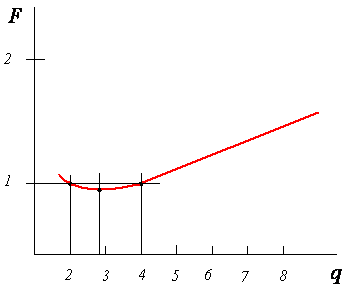
Рис. 1. Зависимость относительного

показателя экономичности

от основания системы счисления

Используя (10), можно доказать, что троичная система счисления экономичнее двоичной. В подавляющем большинстве

ЭВМ используют двоичную систему счисления, однако для ЭВМ это связа­но с преодолением дополнительных трудностей, возникающих при переводе входной информации в двоичную систему счисления и двоичной информации в выходную информацию.

1.1 Перевод числовой информации из одной позиционной

системы в другую

В процессе преобразования информации в цифровом автомате возникает необходимость перевода чисел из одной позиционной системы счисления в другую. Это обусловлено тем, что в качестве внутреннего алфавита наиболее целесообразно использовать двоичный алфавит с символами 0 и 1.

Первым два символа для кодирования информации применил известный философ XVII в. Ф. Бэкон, который использовал символы 0, 1.

Рассмотрим задачу перевода чисел в общей постановке. В соответствии с (3) числа в разных системах счисления можно пред­ставить следующим образом:

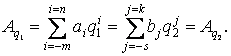(11)

В общем виде задачу перевода числа из системы счисления с основанием q1 в систему счисления с основанием q2 можно представить как задачу определения коэффициентов bi нового ряда, изображающего число в системе с основанием q2. Решить эту задачу можно подбором коэффициентов bi. Основная трудность при этом заключается в выборе максимальной степени, которая еще содержится в числе Аq1 . Все действия должны выполняться по правилам q1 -арифметики, т. е. по правилам исходной системы счисления.