Представление числовой информации в информационных системахРефераты >> Информатика >> Представление числовой информации в информационных системах
Пример 10. Перевести двоичное число А2 = 1011,0111 в восьмеричную систему счисления.
Решение. Исходное число условно разбиваем на триады справа налево для целых чисел и слева направо для правильной дроби. Затем заменяем каждую триаду в соответствии с нижеприведенным соответствием.
Восьмеричная цифра 0 1 2 3 4 5 6 7
Двоичный эквивалент 000 001 010 011 100 101 110 111
A2 = 001 011,011 100.
A8 = 1 3,3 4.
Ответ: А8 = 13,34.
В качестве промежуточных систем счисления целесообразно использовать системы с основанием q = 2k. При этом существенно упрощается преобразование информации из системы счисления с основанием q = 2k в двоичную систему и наоборот. Преобразование фактически сводится к тому, что символы первоначальной информации, заданной в системе с основанием q = 2k, заменяются соответствующими двоичными эквивалентами (см. табл. 1). Представление десятичных чисел в таком виде называется десятично-двоичным. Обратное преобразование из двоичной системы в систему с основанием q = 2k сводится к тому, что двоичный код разбивается на группы по k двоичных разрядов в каждой (начиная от младших разрядов для целых чисел или с первого разряда после запятой для правильных дробей); эти группы (диады, триады, тетрады (табл.2) и т. д.) заменяются соответствующими символами исходной системы счисления. Таблица 2
| Десятичное число | Двоичный эквивалент для q = 24 | Десятичное число | Двоичный эквивалент для q = 24 | Десятичное число | Двоичный эквивалент для q = 24 |
| 0 | 0000 | 6 | 0110 | 11 | 1011 |
| 1 | 0001 | 7 | 0111 | 12 | 1100 |
| 2 | 0010 | 8 | 1000 | 13 | 1101 |
| 3 | 0011 | 9 | 1001 | 14 | 1110 |
| 4 | 0100 | 10 | 1010 | 15 | 1111 |
| 5 | 0101 |
Системы счисления с основанием q = 2k широко используют для записи программ решения задач, а также для ускорения выполнения арифметических операций.
(разновидности систем счисления: с другими символами - (1, -1); избыточная - (0, 1, -1); с отрицательным основанием –(q < 0)).
1.2 Формы представления числовой информации
Число 0,028 можно записать так: 28·10-3, или 0,03 (с округлением), или 2,8·10-2 и т. д. Разнообразие форм в записи одного числа может послужить причиной затруднений для работы цифрового автомата. Во избежание этого нужно либо создать специальные алгоритмы распознавания числа, либо указывать каждый раз форму его записи. Второй путь проще.
Существуют две формы записи чисел: естественная и нормальная. При естественной форме число записывается в естественном натуральном виде, например 12560 — целое число; 0,003572 — правильная дробь; 4,89760 — неправильная дробь. При нормальной форме запись одного числа может принимать разный вид в зависимости от ограничений, накладываемых на ее форму. Например, число 12560 может быть записано так:
12560 = 1,256 · 104 = 0,1256 · 105 = 125600 · 10-1 и т. д.
Автоматное (машинное) изображение числа— представление числа А в разрядной сетке цифрового автомата. Условно обозначим автоматное изображение числа символом [А]. Тогда справедливо соотношение: А = [А]КA, где КA — коэффициент, величина которого зависит от формы представления числа в автомате.
Представление чисел с фиксированной запятой (точкой). Естественная форма представления числа в цифровом автомате характеризуется тем, что положение его разрядов в автоматном изображении остается всегда постоянным независимо от величины самого числа. Существует также другое название этой формы записи чисел — представление чисел с фиксированной запятой (точкой).
Чтобы упростить функционирование цифрового автомата, необходимо ограничить входную информацию какой-то одной областью чисел (на вход автомата желательно подавать либо целые числа, либо правильные дроби, либо любые числа), что позволит определить значения масштабного коэффициента КA. Например, если на вход цифрового автомата поступают только правильные дроби, то
![]() , (19)
, (19)
где [A]ф — машинное изображение числа для формы представления с фиксированной запятой.
Тогда число А будет представлено в виде А = [A]фKA.
Величина масштабного коэффициента КA, удовлетворяющего условию (19), определяет тот факт, что в машинном изображении запятая всегда стоит после целой части дроби, т. е. перед ее старшим разрядом. Следовательно, можно хранить только дробную часть числа (цифровую часть), а в разряде целой части писать дополнительную информацию.
Так как числа бывают положительные и отрицательные, то формат (разрядная сетка) автоматного изображения разбивается на знаковую часть и поле числа (рис.2, а). В знаковую часть записывается информация о знаке. Примем, что знак положительного числа «+» изображается символом 0, а знак отрицательного числа «-» изображается символом 1.
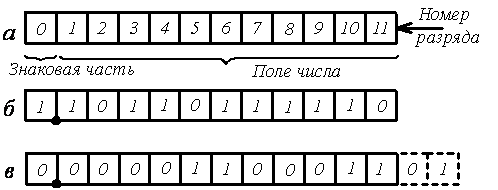
Рис. 2. Представление чисел в форме
с фиксированной запятой
Если на вход цифрового автомата поступают целые числа, например, как в ЕС ЭВМ, то в разрядной сетке (в формате машинного изображения) один разряд отводится под знак числа, а последующие разряды образуют поле числа. Диапазон представимых чисел в этом случае от - (2n -1) до + (2n -1), где п — количество разрядов без знаковой части.
