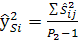,

а для отцовских форм - по формуле:

Например, для сорта Лютесценс 78:

(Лютесценс 78)=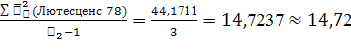

Для аналога БСК-21 (Lr 9):

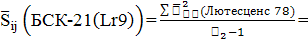7,06027,06

Таким же образом рассчитываем вариансы СКС и по другим родительским формам. Полученные значения сумм квадратов констант и варианс CKC заносим в таблицу8.

Таблица 8 - Квадраты констант (Щ) и вариансы СКС

Для сравнения варианс СКС среди материнских и отцовских форм определим среднюю вариансу СКС отдельно по материнским и отцовским формам В данном случае эти величины будут одинаковы, поскольку Р, = Р2.

Например, для материнских форм:

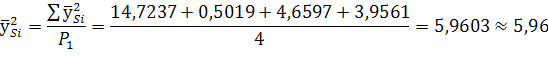
Для отцовских форм:

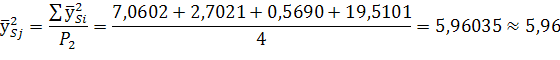
Результаты расчёта варианс СКС также как и эффекты ОКС можно изобразить в виде столбчатой диаграммы (рисунок 3).

2.3.4 Определение варианс эффектов, различий между эффектами и стандартных ошибок

Заключительным этапом анализа комбинационной способности является определение варианс эффектов и различий между эффектами, а также стандартных ошибок. Стандартные ошибки используют для сравнения достоверности определения пределов средних значений и различий между теми или иными эффектами. Варианса случайных отклонений для среднего значения изучаемого признака у любого гибрида будет равна:

где E2 - паралитический эффект, определяемый при дисперсионном анализе исходных данных.

В нашем случае 2 = = 5,04

Варианса разности средних значений признака любых двух гибридов составит:

Вариансы эффектов вычисляем по формулам:

1)

2)

3)

4)

Вариансы разности эффектов вычисляем по формулам:

1)

2)

3)

4)

Стандартные ошибки найдём путём извлечения квадратного корня из варианс эффектов и разностей эффектов. Полученные значения варианс эффектов, различий между ними и стандартные ошибки показаны в таблице 9.