Результаты неэмпирических расчетов тепловых эффектов органических реакций очень сильно зависят от выбора метода. В валентно – расщепленных базисах для реакций с участием насыщенных молекул ошибки составляют около 40 кДж/моль, но, если в молекуле есть кратные связи или молекулы являются напряженными, ошибки обычно увеличиваются приблизительно в 2 раза.

2.1.5 Расчет поверхностей потенциальной энергии

Для получения наиболее полной информации о механизме реакции необходимо вычислить многомерную поверхность потенциальной энергии (ППЭ), то есть рассчитать зависимость полной энергии от координат атомных ядер. Наиболее интересными и важными при изучении механизма реакции являются так называемые стационарные точки на ППЭ. Под этим термином понимают минимумы и седловые точки на ППЭ (рисунок 3.1.5.1, 3.1.5.2) В стационарных точках производные полной энергии по всем независимым координатам равны нулю.

Рисунок 2.1.5.1 Стационарные точки

а — минимум локальный или глобальный;

б — седловая точка

Рисунок 2.1.5.2 Простейшая ППЭ

Темные кружки – исходные

реагенты и продукты реакции;

крестик — переходное состояние.

В точке минимума полной энергии матрица вторых производных имеет только положительные собственные значения, а в седловой точке – одно отрицательное собственное значение. Минимумы полной энергии соответствуют устойчивым структурам и интермедиатам, а седловые точки – переходным состояниям.

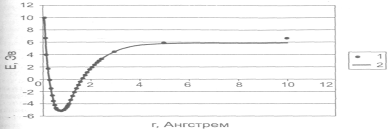
Рисунок 2.1.5.3. Зависимость потенциальной энергии молекулы водорода от расстояния между атомами: 1 — расчет полуэмпирическим методом РМЗ; 2 — аппроксимация потенциалом Морзе.

Типичный вид простейшей двумерной ППЭ показан на рисунке 2.1.5.2. Здесь минимумы соответствуют исходным реагентам и конечным продуктам реакции, а седловая точка – переходному состоянию. Минимумы на рисунке соединены пунктирной линией, которая проходит по дну долины на ППЭ через седловую точку. Эта линия показывает путь реакции в двумерном пространстве или траекторию движения реагентов в ходе реакции. Для большинства реакций ППЭ имеют более сложный вид.

В таблицах 1.7 и 1.8 приложения А сопоставлены данные расчета параметров переходных состояний для реакций, изображенных на схемах 1 - 5, методами МПДП и КМПДП (метод МПДП с учетом электронной корреляции), неэмпирическим методом в приближении Хартри – Фока без учета и с учетом электронной корреляции.

Схема I Схема II Схемa III

Схема IV Схемa V

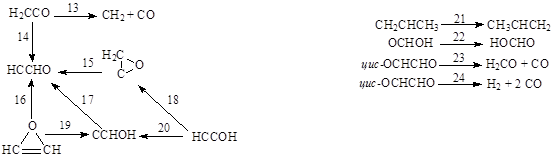
В таблицах неэмпирический расчет в приближении Хартри – Фока без учета электронной корреляции обозначен ХФ, с учетом электронной корреляции – КХФ. Для реакций, изображенных на схемах 1 – 3, расчеты с оптимизацией геометрии в приближении Хартри – Фока проведены в базисе 6-31ГФ*, для реакций, изображенных на схемах 4, 5, - в базисе 3-21ГФ или 4-31ГФ. Электронная корреляция учитывалась только при вычислении энергии активации.

Из этих данных видно, что геометрические параметры переходных состояний, вычисленные методами МПДП и КМПДП, находятся в хорошем согласии с данными неэмпирических расчетов без учета электронной корреляции.

Вопрос о влиянии электронной корреляции на геометрию переходных состояний был рассмотрен в работе Шредера [20]. В ней методом МПДП без учета и с учетом электронной корреляции была рассчитана геометрия переходных состояний для реакций, изображенных на схемах 1 – 5, и показана хорошая сходимость с экспериментом.

2.1.6 Силовые постоянные химических связей и частоты внутримолекулярных колебаний

Для расчета силовых постоянных довольно широко применяют как полуэмпирические, так и неэмпирические методы квантовой химии. В любом случае сначала оптимизируют геометрию, то есть определяют наиболее устойчивую конформацию, отвечающую минимуму полной энергии; затем вычисляют вторые производные полной энергии по естественным координатам, а при необходимости – кубичные и биквадратные члены.

При использовании минимального слейтеровского базиса согласие с экспериментом получается весьма посредственное. Для полуэмпирических методов характерно относительное занижение частот деформационных колебаний по сравнению с валентными. В связи с тем, что ошибки в большинстве случаев носят систематический характер, их удается значительно уменьшить введением эмпирически подобранных масштабных корректирующих множителей для определенных типов силовых постоянных или инкременентов, которые прибавляются к рассчитанным частотам.

Для расчетов методами МЧПДП/3 и МПДП Дьюар и Форд [23] подобрали систему инкрементов, специфичных для валентных, деформационных и торсионных колебаний определенных атомных групп или связей; на очень большом числе примеров продемонстрирована удовлетворительная точность результатов.

сульфаниламид квантовый химический органический молекула

Более логичным представляется корректирование значений силовых постоянных, и на этом пути достигнуты положительные результаты. В настоящее время используется несколько методик подбора корректирующих множителей. Наиболее распространенными являются следующие предложения:

1. Корректировка только диагональных силовых коэффициентов, а недиагональные оставлять без изменений.

2. Использование одного общего корректирующего множителя для всех недиагональных силовых постоянных.

Подбирать значения корректирующих множителей только для диагональных членов, а корректирующие множители для недиагональных коэффициентов вычислять как среднее геометрическое из соответствующих диагональных величин.

2.2 Вывод

В данной главе были рассмотрены возможности программы HyperChem для расчета геометрических и физико–химических параметров молекул и проведена сравнительная оценка используемых методов. Из приведенных выше данных видно, что наибольшей точностью обладают методы ab initio и АМ1. Этими методами и будет производиться расчет соединений сульфаниламидного ряда. Для сравнительной оценки также включен в расчет метод INDO.

В следующей главе будут представлены рассчитанные геометрические параметры молекул сульфаниламидного ряда и рассчитанная физиологическая активность этих соединений. Следует сказать, что вначале проводился расчет геометрии приведенных соединений, затем просчитанные соединения были проверены на наличие физиологической активности.

Глава 3 СУЛЬФАНИЛАМИДНЫЕ ЛЕКАРСТВЕННЫЕ ПРЕПАРАТЫ

3.1 История открытия сульфаниламидов

Сульфаниламидными препаратами называются лекарственные вещества, содержащие сульфамидную группу, большей частью производные бензосульфамида (1). Простейшим из них является п – аминобензолсульфамид (2) сульфаниламид или амид сульфониловой кислоты. Он впервые синтезирован Гельмо в 1908 году среди других производных анилина. В 1909 году были сделаны попытки использования сульфаниламида в качестве диазосоставляющей азокрасителей (для шерсти).