Оптимизация процессов бурения скважин
|
№ |
Интервал |
Среднее значение |
Частота |
|
1 |
3,8 – 3,95 |
3,875 |
2 |
|
2 |
3,95 – 4,10 |
4,025 |
2 |
|
3 |
4,10– 4,25 |
4,175 |
3 |
|
4 |
4,25 – 4,4 |
4,325 |
2 |
1. Сравнение с теоретической кривой.
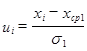- параметр функции 
, где
- среднее значение на интервале;
2. Рассчитываем для каждого интервала 
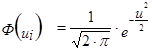- функция плотности вероятности нормально распределения;
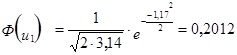
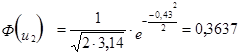
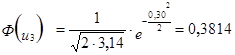
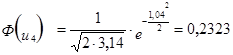
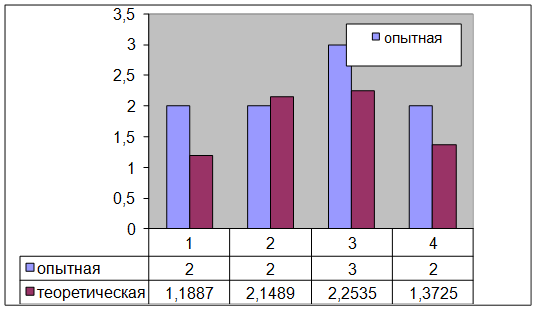
3. Расчёт теоретической частоты.
- теоретическая частота в i-том интервале.
|
№ |
|
|
|
|
|
|
|
|
1 |
3,88 |
2 |
-1,1694 |
0,2012 |
1,1887 |
0,6582 |
0,5537 |
|
2 |
4,04 |
2 |
-0,4310 |
0,3637 |
2,1489 |
0,0222 |
0,0103 |
|
3 |
4,2 |
3 |
0,3077 |
0,3814 |
2,2535 |
0,5572 |
0,2473 |
|
4 |
4,34 |
2 |
1,0460 |
0,2323 |
1,3725 |
0,3937 |
0,2869 |
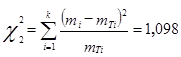
- число степеней свободы;
- порог чувствительности;
- вероятность;
Если 
, то данные эксперимента согласуются с нормальным законом распределения, где 
- табличное значение критерия Пирсона.
Если
- данные эксперимента не согласуются с нормальным законом распределения, необходимо дальнейшее проведение опытов. Поскольку вычисленное значение (
) превосходит табличное значение критерия Пирсона, то данные эксперимента не согласуются с нормальным законом распределения.
45. Определение доверительного интервала
Форма распределения Стьюдента зависит от числа степеней свободы.
где 
коэффициент Стьюдента
Выборка №1
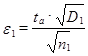
где 
- при вероятности 
и числе опытов 
.
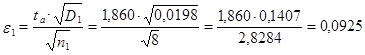
Выборка №2
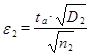
где 
- при вероятности и числе опытов .
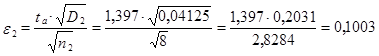
Доверительные интервалы
Выборка №1
Интервал 3,945 - 4,0375 - 4,13.
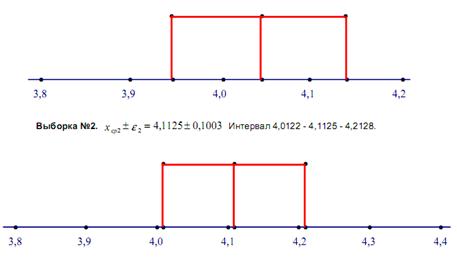
46.Дисперсионный анализ
Основной целью дисперсионного анализа является исследование значимости различия между средними. В нашем случае мы просто сравниваем средние в двух выборках. Дисперсионный анализ даст тот же результат, что и обычный 
- критерий для зависимых выборок (сравниваются две переменные на одном и том же объекте).
