Оптимизация процессов бурения скважин
Значения выборки 2 выходят за границы критического интервала отбраковки.
В выборке №1 и №2 по методу Башинского значение выборки вышло за границы критического интервала отбраковки, поэтому 
и 
подлежат отбраковки. Теперь пересчитаем среднюю величину для обоих выборок.
13.Расчёт средней величины
|
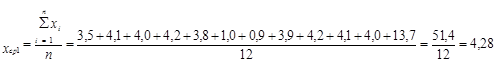
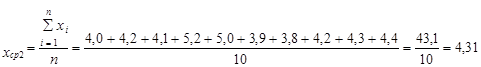
Выборка №1 |
Выборка №2 | ||||
|
1 |
3,5 |
0,6084 |
1 |
4,0 |
0,0961 |
|
2 |
4,1 |
0,0324 |
2 |
4,2 |
0,0121 |
|
3 |
4,0 |
0,0784 |
3 |
4,1 |
0,0441 |
|
4 |
4,2 |
0,0064 |
4 |
5,2 |
0,7921 |
|
5 |
3,8 |
0,2304 |
5 |
5,0 |
0,4761 |
|
6 |
1,0 |
10,7584 |
6 |
3,9 |
0,1681 |
|
7 |
0,9 |
11,4244 |
7 |
3,8 |
0,2601 |
|
8 |
3,9 |
0,1444 |
8 |
4,2 |
0,0121 |
|
9 |
4,2 |
0,0064 |
9 |
4,3 |
0,0001 |
|
10 |
4,1 |
0,0324 |
10 |
4,4 |
0,0081 |
|
11 |
4,0 |
0,0784 | |||
|
12 |
13,7 |
88,7364 | |||
|
Среднее значение |
4,28 |
112,1368 |
Среднее значение |
4,31 |
1,869 |
|
Дисперсия |
10,194 |
Дисперсия |
0,2076 | ||
14.Расчёт дисперсии
15. Расчёт среднеквадратичной величины.
16. Расчёт коэффициента вариации.
17. Определение размаха варьирования.
18.Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1
Значения выборки 1 не выходят за границы критического интервала отбраковки.
Выборка №2
Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2
Значения выборки 2 выходят за границы критического интервала отбраковки.
В выборке №1 и №2 по методу Башинского значение выборки вышло за границы критического интервала отбраковки, поэтому и 
подлежат отбраковки. Теперь пересчитаем среднюю величину для обоих выборок.
19. Расчёт средней величины
|
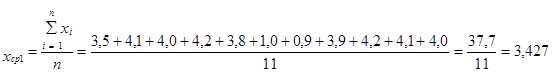
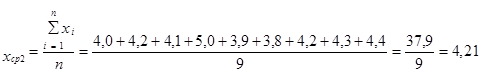
Выборка №1 |
Выборка №2 | ||||
|
1 |
3,5 |
0,005329 |
1 |
4,0 |
0,0441 |
|
2 |
4,1 |
0,452929 |
2 |
4,2 |
0,0001 |
|
3 |
4,0 |
0,328329 |
3 |
4,1 |
0,0121 |
|
4 |
4,2 |
0,597529 |
4 |
5,0 |
0,6241 |
|
5 |
3,8 |
0,139129 |
5 |
3,9 |
0,0961 |
|
6 |
1,0 |
5,890329 |
6 |
3,8 |
0,1681 |
|
7 |
0,9 |
6,385729 |
7 |
4,2 |
0,0001 |
|
8 |
3,9 |
0,223729 |
8 |
4,3 |
0,0081 |
|
9 |
4,2 |
0,597529 |
9 |
4,4 |
0,0361 |
|
10 |
4,1 |
0,452929 | |||
|
11 |
4,0 |
0,328329 | |||
|
Среднее значение |
3,427 |
15,401819 |
Среднее значение |
4,21 |
0,9889 |
|
Дисперсия |
1,5401819 |
Дисперсия |
0,1236125 | ||
