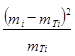Оптимизация процессов бурения скважин
42. Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1
Метод Башинского:
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
43. Определение предельной относительной ошибки испытаний.
Выборка №1
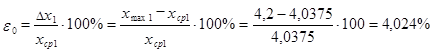
Выборка №2
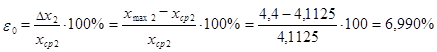
44. Проверка согласуемости экспериментальных данных с нормальным законом распределения при помощи критерия Пирсона.
|
№ |
Интервал |
Среднее значение |
Частота |
|
1 |
3,8 – 3,9 |
3,85 |
1 |
|
2 |
3,9 – 4,0 |
3,95 |
3 |
|
3 |
4,0 – 4,1 |
4,05 |
2 |
|
4 |
4,1 – 4,2 |
4,15 |
2 |
Выборка №1 Определим количество интервалов:
где 
- размер выборки 1
1. Сравнение с теоретической кривой.
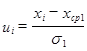- параметр функции 
где
- среднее значение на интервале;
2. Рассчитываем для каждого интервала 
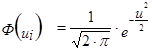- функция плотности вероятности нормально распределения;
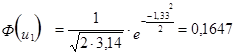
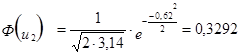
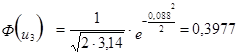
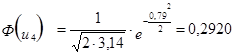
3. Расчёт теоретической частоты.
- теоретическая частота в i-том интервале.
|
№ |
|
|
|
|
|
|
|
|
1 |
3,85 |
1 |
-1,332 |
0,1647 |
0,9364 |
0,0040 |
0,004 |
|
2 |
3,95 |
3 |
-0,622 |
0,3292 |
1,8717 |
1,2730 |
0,680 |
|
3 |
4,05 |
2 |
0,088 |
0,3977 |
2,2612 |
0,0682 |
0,030 |
|
4 |
4,15 |
2 |
0,799 |
0,2920 |
1,6603 |
0,3397 |
0,204 |
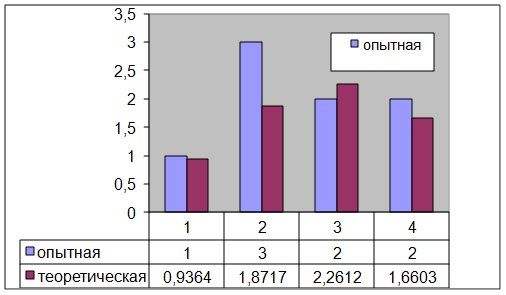
Число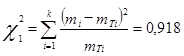 
подчиняется 
- закону Пирсона
- число степеней свободы;
- порог чувствительности;
- вероятность;
Если 
, то данные эксперимента согласуются с нормальным законом распределения, где 
- табличное значение критерия Пирсона.
Если
- данные эксперимента не согласуются с нормальным законом распределения, необходимо дальнейшее проведение опытов. Поскольку вычисленное значение (
) превосходит табличное значение критерия Пирсона, то данные эксперимента не согласуются с нормальным законом распределения.
Выборка №2
Определим количество интервалов:
, где 
- размер выборки 2
