Оптимизация процессов бурения скважин
Выборка №2
Значения выборки 2 не выходят за границы критического интервала отбраковки.
В выборке №1 по методу Башинского значение выборки вышло за границы критического интервала отбраковки, поэтому 
подлежит отбраковки. Теперь пересчитаем среднюю величину для выборки №1.
31.Расчёт средней величины.
|
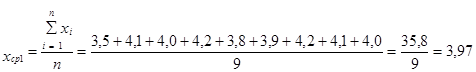
Выборка №1 |
Выборка №2 | ||||
|
1 |
3,5 |
0,2282716 |
1 |
4,0 |
0,01265625 |
|
2 |
4,1 |
0,0149382 |
2 |
4,2 |
0,00765625 |
|
3 |
4,0 |
0,0004938 |
3 |
4,1 |
0,00015625 |
|
4 |
4,2 |
0,0493827 |
4 |
3,9 |
0,04515625 |
|
5 |
3,8 |
0,0316049 |
5 |
3,8 |
0,09765625 |
|
6 |
3,9 |
0,0060494 |
6 |
4,2 |
0,00765625 |
|
7 |
4,2 |
0,0493827 |
7 |
4,3 |
0,03515625 |
|
8 |
4,1 |
0,0149382 |
8 |
4,4 |
0,08265625 |
|
9 |
4,0 |
0,0004938 | |||
|
Среднее значение |
3,97 |
0,395555 |
Среднее значение |
4,1125 |
0,28875625 |
|
Дисперсия |
0,049 |
Дисперсия |
0,04 | ||
32.Расчёт дисперсии.
33. Расчёт среднеквадратичной величины.
34. Расчёт коэффициента вариации.
35. Определение размаха варьирования.
36. Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1 
Метод Башинского:
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
В выборке №1 по методу Башинского значение выборки вышло за границы критического интервала отбраковки, поэтому подлежит отбраковки. Теперь пересчитаем среднюю величину для выборки №1.
37. Расчёт средней величины.
|
Выборка №1 |
Выборка №2 | ||||
|
1 |
4,1 |
1 |
4,0 |
0,01265625 | |
|
2 |
4,0 |
2 |
4,2 |
0,00765625 | |
|
3 |
4,2 |
3 |
4,1 |
0,00015625 | |
|
4 |
3,8 |
4 |
3,9 |
0,04515625 | |
|
5 |
3,9 |
5 |
3,8 |
0,09765625 | |
|
6 |
4,2 |
6 |
4,2 |
0,00765625 | |
|
7 |
4,1 |
7 |
4,3 |
0,03515625 | |
|
8 |
4,0 |
8 |
4,4 |
0,08265625 | |
|
Среднее значение |
4,0375 |
Среднее значение |
4,1125 |
0,28875625 | |
|
Дисперсия |
Дисперсия |
0,04 | |||
38. Расчёт дисперсии.
39. Расчёт среднеквадратичной величины.
40. Расчёт коэффициента вариации.
41. Определение размаха варьирования.
