Оптимизация процессов бурения скважин
Выборка №2
Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
,
где
- коэффициент Башинского;
- размах варьирования.
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2
Значения выборки 2 выходят за границы критического интервала отбраковки.
В выборке №1 и №2 по методу Башинского значение выборки вышло за границы критического интервала отбраковки, поэтому 
и 
подлежат отбраковки. Теперь пересчитаем среднюю величину для обоих выборок.
7. Расчёт средней величины
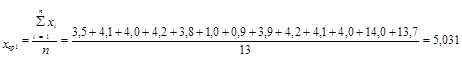
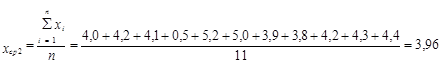
8. Расчёт дисперсии
|
Выборка №1 |
Выборка №2 | ||||
|
1 |
3,5 |
2,343961 |
1 |
4,0 |
0,0016 |
|
2 |
4,1 |
0,866761 |
2 |
4,2 |
0,0576 |
|
3 |
4,0 |
1,062961 |
3 |
4,1 |
0,0196 |
|
4 |
4,2 |
0,690561 |
4 |
0,5 |
11,9716 |
|
5 |
3,8 |
1,515361 |
5 |
5,2 |
1,5376 |
|
6 |
1,0 |
16,248961 |
6 |
5,0 |
1,0816 |
|
7 |
0,9 |
17,065161 |
7 |
3,9 |
0,0036 |
|
8 |
3,9 |
1,279161 |
8 |
3,8 |
0,0256 |
|
9 |
4,2 |
0,690561 |
9 |
4,2 |
0,0576 |
|
10 |
4,1 |
0,866761 |
10 |
4,3 |
0,1156 |
|
11 |
4,0 |
1,062961 |
11 |
4,4 |
0,1936 |
|
12 |
14,0 |
80,442961 | |||
|
13 |
13,7 |
75,151561 | |||
|
Среднее значение |
5,031 |
199,287693 |
Среднее значение |
3,96 |
15,0656 |
|
Дисперсия |
16,60730775 |
Дисперсия |
1,50656 | ||
9. Расчёт среднеквадратичной величины
10.Расчёт коэффициента вариации.
11. Определение размаха варьирования
12.Отбраковка непредставительных результатов измерений.
Метод 3s:
Выборка №1
Значения выборки 1 не выходят за границы критического интервала отбраковки.
Выборка №2
Значения выборки 2 не выходят за границы критического интервала отбраковки.
Метод Башинского:
Выборка №1
Значения выборки 1 выходят за границы критического интервала отбраковки.
Выборка №2
