Неоднородные плоские волны играют главенствующую роль в образовании преломленной (головной) волны, которую рассмотрим несколько позже в отдельном разделе. Здесь подчеркнем одно - все особенности неоднородной волны выявлены в результате анализа лишь волнового аргумента проходящей волны при закритическом падении плоской волны на границу раздела. Вид самой волновой функции этим анализом не затронут. Поэтому вернемся к исследованию поведения спектральных коэффициентов рассеивания и вторичных волн при закритическом падении первичной волны.

Итак, установлено, что при

где

.

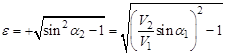Коэффициенты рассеивания А и В в этом случае описываются выражениями:

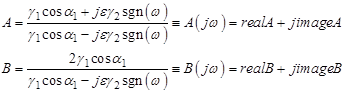
Знаком тождества подчеркнута комплексная зависимость коэффициентов рассеивания от частоты, оправдывающая введенное ранее определение А и В как спектральных коэффициентов рассеивания.

В числителе и знаменателе дроби, определяющей А - комплексно-сопряженные выражения: , имеющие одинаковый модуль (так как ) и противоположные по знаку аргументы. Поэтому модуль спектрального коэффициента выражения равен 1:

и не зависит ни от частоты, ни от угла падения. Фазово-частотный коэффициент отражения как аргумент дроби с комплексно-сопряженными числителем и знаменателем, равен:

.

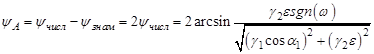Действительная realA и мнимая imageA части спектрального коэффициента отражения (СКО) равны:

,

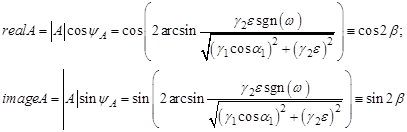где

.

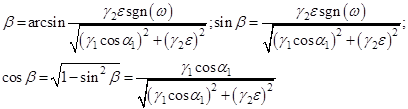Используя формулы косинуса и синуса двойного угла (), получим выражения для действительной и мнимой частей СКО в виде:

;

.

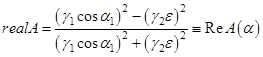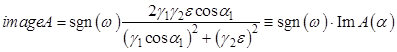Действительная часть СКО не зависит от частоты, а зависимость мнимой части от нее задается множителем в виде знаковой функции частоты. Обе части СКО являются функциями угла падения. Спектральная характеристика отражения обладает всеми свойствами устойчивой линейной системы - четными амплитудно-частотной характеристикой (модулем СКО) и действительной части СКО, и нечетными фазово-частотной характеристикой (аргументом СКО) и мнимой частью СКО. При этом, четность обеспечивается отсутствием зависимости и realA от частоты, а нечетность и imageA - множителем в виде знаковой функции sgn (ω). Таким образом, комплексный спектральный коэффициент отражения может быть записан в виде:

.

Спектр отраженной волны разделяется на два слагаемых:

.

В первом слагаемом присутствует спектр первичной волны с амплитудным множителем (весом) ReA (α), независимым от частоты и меняющимся с увеличением угла падения.

Во втором слагаемом - произведение двух частотно-зависимых функций - знаковой и комплексного спектра первичной волны u (jf) - с амплитудным множителем ImA (α), также изменяющимся с увеличением угла падения.

Так как преобразование Фурье - линейная операция, сам отраженный сигнал также является взвешенной суммой Фурье-трансформант слагаемых своего спектра:

.

Здесь - результат обратного Фурье-преобразования знаковой функции частоты sgn (f), u (t) u (jf), а произведение спектров заменено сверткой Фурье-трансформант сомножителей в соответствии со спектральной теоремой свертывания функций.

В теории спектров рассматривалась знаковая функция времени sgn (t) и ее спектр:

.

Аналогично определяется обратное Фурье-преобразование знаковой функции частоты:

.

Здесь появился знак минус как следствие противоположных знаков ядер прямого () и обратного () преобразований Фурье.

Тогда отраженный сигнал может быть описан выражением:

.

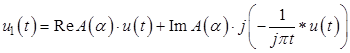Сокращая мнимую единицу и раскрывая символьную запись свертки, получим описание отраженного сигнала при углах падения, превышающих критический угол:

.

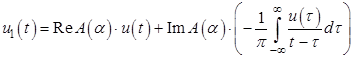В скобках записано обратное Гильберт-преобразование функции u (t), описывающей первичную волну:

.

Таким образом, отраженный сигнал за критическим углом падения представляется взвешенной суммой падающего сигнала u (t) и его Гильберт-трансформанты :

.

Веса слагаемых - ReA (α) и ImA (α) - изменяются при увеличении угла падения. Соответственно, изменяется по форме и суммарный отраженный сигнал .

Проведем анализ зависимости от угла падения α весовых множителей ReA (α) и ImA (α) и структуры суммарной отраженной волны при изменении α от критического угла до теоретически возможного предела 90°. Как отмечалось, при α = А () = 1 = ReA (), ImA () = 0. Отраженная волна имеет те ж форму и амплитуду, что и падающая волна: = .

Как только угол падения превысит критический угол, ReA (α) стремительно уменьшается, а мнимая часть ImA (α) столь же быстро возрастает. Доля первичного сигнала в суммарной отраженной волне быстро уменьшается, и так же быстро растет доля Гильберт-трансформанты падающей волны. При некотором угле падения действительная часть спадает до 0, а мнимая - возрастает до 1: