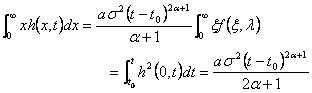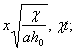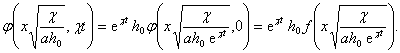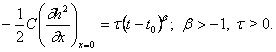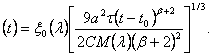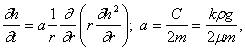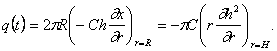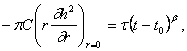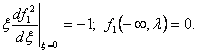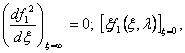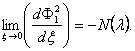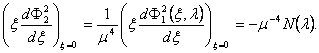Физическое описание явления фильтрации жидкости
![]()
(47)
Уравнения (46) и (47) были даны Буссинеском.
2.4. Основные уравнения фильтрации газа
При исследовании фильтрации газа основное значение имеет тот факт, что сжимаемость газа обычно на несколько порядков превышает сжимаемость пористой среды. С учетом этого обстоятельства в уравнении неразрывности
|
(48)
изменением пористости m во времени можно пренебречь, так что получим
|
(49)
Для того чтобы получить замкнутую систему уравнений, снова нужно использовать связь плотности газа r с его давлением р и температурой Т:
r = r(р,Т), (50)
поэтому в задаче появляется новая переменная Т, и для замыкания системы уравнений нужно добавить еще одно уравнение - уравнение энергии. Однако, если в среде отсутствуют источники выделения или поглощения энергии, то изменения температуры в процессе движения газа крайне малы, и при расчете поля давления газа ими можно пренебречь. Это обстоятельство легко понять, если учесть, во-первых, крайнюю малость скорости фильтрации и, во-вторых, наличие теплового балласта - скелета пористой среды, эффективно подавляющего изменения температуры. Будем поэтому считать, что
r = r(р,Т0)= r(р), (51)
где Т0 - постоянная температура.
Присоединяя к уравнениям (49) и (51) уравнение закона фильтрации (предполагаемого линейным)
|
(52)
получаем замкнутую систему уравнений. Исключая скорость фильтрации, имеем
|
(53)
В уравнении (53) r - известная функция давления. Аналогично и вязкость газа, зависящая в общем случае от давления и температуры, может быть представлена в виде:
m = m(р,Т0) =m(р). (54)
Таким образом, и вязкость может считаться известной функцией одного лишь давления.
Введем теперь функции
|
(55)
Уравнение (53) принимает при этом вид:
|
(56)
Можно показать, что уравнение для давления сохранит форму (56) и в случае, если учитывается деформируемость пористой среды, т. е. зависимость от давления пористости и проницаемости (среда по-прежнему считается однородной).
В простейшем случае, когда газ можно считать термодинамически идеальным, с вязкостью, не зависящей от давления,
|
m = const, (57)
(р0 и r0 - постоянные). При этом
|
(58)
и уравнение (56) преобразуется к виду:
|
(59)
или
|
Уравнения (59) и (60) выведены в предположении постоянства температуры газа Т0. Поэтому их обычно называют уравнениями изотермической фильтрации газа.
Уравнение (60) - основное для теории фильтрации газа - получено впервые Л. С. Лейбензоном, а затем, несколько позднее, в работе Маскета и Ботсета. Преобразования (55) также берет свое начало от работ Л. С. Лейбензона. Далее уравнение (60) совпадает с уравнением Буссинеска (47) для напора при пологих безнапорных фильтрационных движениях. Эта аналогия, впервые обнаруженная Л. С. Лейбензоном, позволяет рассматривать исследование изотермической фильтрации газа и пологих безнапорных движений несжимаемой жидкости как одну задачу.
3. НЕЛИНЕЙНЫЕ ИНВАРИАНТНЫЕ ЗАДАЧИ
НЕСТАЦИОНАРНОЙ ФИЛЬТРАЦИИ
ЖИДКОСТЕЙ И ГАЗОВ
3.1. Общая характеристика инвариантных задач
теории нестационарной фильтрации.
Автомодельные пологие безнапорные движения
при нулевом начальном уровне жидкости
3.3.1. Общая характеристика инвариантных задач теории нестационарной фильтрации. В разделе 2 было показано, что основные задачи гидродинамической теории нестационарной фильтрации приводят к краевым, смешанным или начальным задачам для нелинейных, как правило, дифференциальных уравнений в частных производных параболического типа. Нелинейность вообще характерна для многих актуальных задач современной гидродинамики: газодинамики, теории волн, теории движений вязкой жидкости и т. д. В настоящее время существует сколько-нибудь общих эффективных аналитических методов решения достаточно широких классов нелинейных задач математической физики; это в полной мере относится и к теории фильтрации. Поэтому в теории фильтрации уже давно привлекли внимание своеобразные частные решения, которые выражаются через функции одной переменной. Вначале эти решения обратили на себя внимание только потому, что их получение сводилось к решению обыкновенных уравнений и представлялось (особенно в домашинную эру) более простым, чем решение уравнений в частных производных в общем случае. При построении различных приближенных методов решения, более общих, эти решения часто использовались как эталоны, позволяющие оценить точность метода. (Приближенные методы аналитического решения сохраняют, особенно в теории фильтрации, свое значение и сейчас, при широком внедрении машин, поскольку эти методы дают аналитические формулы, позволяющие наглядно проследить влияние различных параметров, а высокая точность в теории фильтрации не представляет особого интереса. В ряде случаев задачи, описываемые такими решениями, представляют и самостоятельный интерес.
Однако главная ценность таких решений была осознана позднее. Оказалось, что они представляют собой асимптотические представления решений весьма широких классов задач именно там, где детальная структура граничных и начальных условий перестает быть существенной, а эти области часто бывают наиболее интересными (например, спустя некоторое время после начала отбора из скважины, пока воронка депрессии не достигла области влияния соседней скважины и т. д.). Поэтому, зная такие решения, мы фактически получаем возможность судить, по крайней мере качественно, о поведении очень широкого класса фильтрационных движений.
Важным свойством рассматриваемых ниже решений является их инвариантность: для одних из этих решений - “автомодельных” - распределение давлений, напоров, плотностей и т. п. оказывается все время подобным самому себе, для других - перемещается как твердое тело с постоянной скоростью и т. д. Это свойство связано с особым характером задач, приводящих к таким решениям. Выполнение определенных преобразований зависимых и независимых переменных оставляет уравнения, граничные и начальные условия задачи неизменными. Как говорят в математике, эти задачи инвариантны относительно некоторой группы непрерывных преобразований. Такие задачи называются инвариантными, они рассматриваются ниже.
3.1.2. Автомодельные пологие безнапорные движения при нулевом начальном уровне жидкости. Ниже будут рассмотрены точные решения некоторых линейных задач нестационарной фильтрации, характеризующихся нулевым начальным условием. Исследование этого класса движений представляет, помимо непосредственного, также принципиальный интерес, поскольку в подобных задачах наиболее сильно проявляется существенно нелинейный характер рассматриваемой проблемы и обнаруживаются некоторые свойства нелинейных движений, резко отличающие их от соответствующих линейных задач и неизбежно утрачиваемые при линеаризации.
Будем рассматривать безнапорные пологие фильтрационные движения в первоначально сухом грунте, имея в виду, что в силу обнаруженной Л. С. Лейбензоном аналогии все результаты непосредственно переносятся на задачи изотермической фильтрации газа. Излагаемые ниже в этом параграфе решения были получены Г. И. Баренблаттом.
Рассмотрим полубесконечный пласт, имеющий снизу плоскую горизонтальную непроницаемую границу - водоупор, а со стороны канала - плоскую вертикальную границу, перпендикулярную оси x и проходящую через точку x =0.
Пусть начальный напор жидкости в пласте равен нулю, а напор на вертикальной границе пласта изменяется по степенному закону, начиная с исходного момента t =t0:
h(0, t) = s (t-t0)a, (61)
где s > 0, а a - некоторая константа, которую будем выбирать в пределах –Ѕ<α<8. В частности, константа a может равняться нулю; в этом случае напор на границе мгновенно принимает некоторое значение s и остается постоянным.
В случае фильтрации газа сформулированная задача отвечает закачке газа в первоначально не заполненный однородный пласт постоянной мощности при изменении давления газа в начальном сечении пласта х = 0 по закону (61). Линиями равных напоров будут линии х = const, параллельные границе пласта. Таким образом, напор h(x, t) удовлетворяет уравнению
|
(62)
получающемуся из общего уравнения Буссинеска (47) для данных геометрических условий задачи, а также граничному условию (61), начальному условию и условию на бесконечности:
h(x, t0) = h(¥, t) = 0. (63)
 Напор в некоторой точке пласта h зависит от следующих аргументов: координаты х, времени, прошедшего от начало процесса t - t0 (в силу однородности уравнения (62) по времени напор будет зависеть только от разности t - t0, а не от значений t и t0 в отдельности), коэффициентов a и s и константы a. Вводя для удобства независимую размерность напора (это возможно, так как для рассматриваемой задачи несущественно, что размерности длины и напора одинаковы), получим размерности этих аргументов в следующем виде:
Напор в некоторой точке пласта h зависит от следующих аргументов: координаты х, времени, прошедшего от начало процесса t - t0 (в силу однородности уравнения (62) по времени напор будет зависеть только от разности t - t0, а не от значений t и t0 в отдельности), коэффициентов a и s и константы a. Вводя для удобства независимую размерность напора (это возможно, так как для рассматриваемой задачи несущественно, что размерности длины и напора одинаковы), получим размерности этих аргументов в следующем виде:
[a] = [h]-1 L2 T-1; [t - t0] = T; [x] = L; [s] = [h] T-a, (64)
где через [h], L и Т обозначены соответственно размерности напора, длины и времени; константа a безразмерна. Из аргументов, от которых зависит напор жидкости, можно составить только две независимые безразмерные комбинации:
|
(65)
В силу p- теоремы анализа размерностей выражение для напора можно представить в виде произведения комбинации определяющих параметров, имеющей размерность напора (в качестве нее можно взять s (t - t0)a ), на безразмерную функцию от безразмерных комбинаций (65). Имеем таким образом
h = s(t - t0)a f(x, l); l = a/(1+a), (66)
где f - безразмерная функция, а параметр l введен вместо параметра a для удобства последующего изложения. Очевидно, что l лежит в интервале -1 <l<1. Имеем, далее, в силу (66)
 |
Подставляя эти соотношения в уравнение (62) и упрощая, получаем для функции f обыкновенное дифференциальное уравнение:
|
(67)
После подстановки выражения (66) в граничное условие (61) и условие (63) получаем для функции f (x, l) краевые условия:
f(0, l) = 1; (68)
f(¥, l) = 0. (69)
Напор и объемный поток (расход) грунтовых вод должны быть непрерывными функциями x и t. Используя закон Дарси, имеем для расхода, приходящего на единицу ширины пласта, выражение
|
(70)
Таким образом, из требования непрерывности расхода следует непрерывность функции df2/dx.
При непрерывной функции f(x) и f ¹ 0 требование непрерывности функции df2/dx = 2fdf/dx совпадает с требованием непрерывности производной df/dx. Однако при f = 0 из непрерывности df2/dx непрерывность df/dx не вытекает. Напротив, как увидим далее, искомая функция f(x, l) имеет в точке, где f обращается в нуль, разрыв первой производной.
Условие (69) удобнее привести к другому виду. Умножим обе части основного уравнения (62) на х и проинтегрируем по х от нуля до бесконечности. В результате получим
|
Очевидно, что dh2/dx стремится к нулю при х®¥, быстрее, чем х-1, в противном случае h не стремилось бы к нулю при х®¥. Используя это обстоятельство и условие на бесконечности (63), получаем
|
Интегрируя это соотношение в пределах от t = t0 до t и используя граничное условие (61) и представление решения (66), имеем
|
(напомним, что считаем a удовлетворяющим неравенству -1/2<a< ¥), откуда получаем искомое условие в форме
|
(71)
В интересующей нас области изменения a и l правая часть (71) конечна и положительна.
3.2. ПОЛОГИЕ БЕЗНАПОРНЫЕ ДВИЖЕНИЯ
С НУЛЕВЫМ НАЧАЛЬНЫМ НАПОРОМ:
ПРЕДЕЛЬНЫЕ АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ,
ОСЕСИММЕТРИЧНЫЕ АВТОМОДЕЛЬНЫЕ ДВИЖЕНИЯ
3.2.1. Предельные автомодельные движения. Рассмотрим теперь для того же полубесконечного пласта несколько иную задачу. Будем исследовать движение на полубесконечном интервале времени (-¥, t), поэтому начальное распределение напора по пласту несущественно.
Предположим, что на больших расстояниях от границы пласта, т.е. при х® ¥, напор жидкости равен нулю; следовательно,
h(¥, t) = 0. (72)
Пусть, далее, напор жидкости на границе пласта возрастет со временем по экспоненциальному закону:
h(0, t) = h0eht. (73)
Напор жидкости внутри пласта h(x, t) по-прежнему удовлетворяет уравнению
|
(74)
Составим полный список аргументов, от которых зависит это решение. Помимо координаты х и времени t, в этот список войдут также величины h0, == и a. Тогда размерности всех определяющих параметров решения представляются в виде:
[x]=L; [t]=T; [a]=[h]-1L2T-1; [h0]=[h]; [c]=T-1, (75)
где по-прежнему символы L, T и [h] означают соответственно размерности длины, времени и напора. Из пяти аргументов (75) с тремя независимыми размерностями можно составить две независимые комбинации, которые удобно взять в виде:
|
|
(76)
где j - безразмерная функция.
Положим теперь t = t¢ + t , где t - произвольная константа. При этом условие (72) и уравнение (74), как нетрудно проверить, записываются через новую переменную t¢, так же как и через прежнюю переменную, а условие (73) принимает вид:
|
Таким образом, сдвиг во времени влияет лишь на некоторое преобразование величины h0, и постановка задачи оказывается по отношению к группе преобразований переноса по времени; для определения h в переменных х, t¢, a, c, h¢0 получается та же задача, что и для определения h в переменных (75). Стало быть, на основе соотношений (76) и (77) имеем
|
(78)
|
(79)
Положим теперь t = t и получим
|
Итак, функция h, зависящая от пяти аргументов (75), представляется через функцию одного аргумента:
|
(81)
Подставляя (81) в основное уравнение (74), получаем для функции f(x) обыкновенное дифференциальное уравнение
|
(82)
Подставляя выражение (81) в условие на бесконечности (72) и граничное условие (73), имеем граничные условия для функции f(x):
f(0) = 1; f(¥) = 0. (83)
В силу непрерывности напора жидкости и потока жидкости функция f(x) по-прежнему должна быть непрерывной и иметь непрерывную производную от квадрата df2/dx. Мы получили, таким образом, для определения функции f(x) граничную задачу того же типа, что и граничные задачи для автомодельных решений, рассмотренных в предыдущем параграфе, и соответствующую значению параметра a, равному бесконечности, т. е. l = 1. Функция f(x) = f(x, 1) тождественно равна нулю при x ³ x0 = 1,810; передний фронт х0 (t) перемещается, таким образом, по закону
|
(84)
а скорость его перемещения равна
|
(85)
Полученное решение является в некотором смысле предельным для автомодельных решений, рассмотренных выше. В самом деле, положим в формуле (66)
s = h0 (at )-a, (86)
где h0 - константа размерности напора; t - константа размерности времени, причем, очевидно, эти константы выбираются с точностью до некоторого постоянного множителя. Решение (66) принимает вид
|
(87)
Будем неограниченно увеличивать в этом решении a при начальном моменте t0 ® - ¥ по закону
t0 = - at. (88)
Раскрывая неопределенность, получаем, что при a ® ¥
|
(89)
Уравнение (67) в пределе при a ® ¥ переходит в уравнение (82), а условия (68) и (69) совпадают с условиями (83); f(x, l) ® f(x, 1) = f(x).
Обозначая t через 1/c, получаем, что при a ® ¥ решение (87) стремится к решению (81). Поэтому решение (81) было названо предельным автомодельным решением. Это решение было получено в работе Г. И. Баренблатта. предельные автомодельные решения представляют и принципиальный интерес в том отношении, что для доказательства автомодельности этих решений уже недостаточно соображений анализа размерности, т. е. недостаточно инвариантности постановки задачи относительно группы преобразования подобия величин с независимыми размерностями, как это было в ранее рассмотренных автомодельных задачах, а требуется дополнительно воспользоваться инвариантностью постановки задачи относительно еще одной группы - группы преобразований переноса по времени.
Приведенные при рассмотрении предельной автомодельной задачи рассуждения носят общий характер и могут применяться во многих других задачах. Очевидно, что предельные автомодельные движения существуют всегда, если система основных уравнений рассматриваемой задачи имеет автомодельные решения обычного степенного типа с произвольным показателем степени (который может принимать сколь угодно большие значения) и инвариантна относительно преобразования переноса соответствующей координаты. Как пример можно указать задачу пограничного слоя в несжимаемой жидкости, а также задачу одномерных неустановившихся движений газа. Полученные для этих задач автомодельные решения, содержащие степенные функции независимых переменных, при предельном переходе, аналогичном проделанному в рассматриваемой задаче теории фильтрации, дают предельные автомодельные решения, полученные Гольдштейном и Станюковичем путем формальной постановки.
|
(90)
Начальный напор во всем пласте равен нулю.
Решение задачи представляется в виде:
|
(91)
где м (l) =-df2(0, l)/dx , а координата переднего фронта жидкости х0 (t) - в виде:
|
2. Осесимметричные автомодельные движения. При осесимметричных пологих безнапорных движениях жидкости напор жидкости h удовлетворяет уравнению
|
(93)
где r - расстояние рассматриваемой точки пласта от оси симметрии.
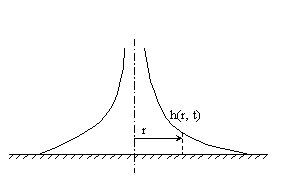 Рассмотрим следующую задачу. Пусть в бесконечный пласт, ограниченный снизу непроницаемой горизонтальной поверхностью - водоупором, через скважину, радиус которой пренебрежимо мал, начинается закачка жидкости. Предположим, что начальный напор жидкости в пласте равен нулю, так что начальное условие на бесконечности имеют вид:
Рассмотрим следующую задачу. Пусть в бесконечный пласт, ограниченный снизу непроницаемой горизонтальной поверхностью - водоупором, через скважину, радиус которой пренебрежимо мал, начинается закачка жидкости. Предположим, что начальный напор жидкости в пласте равен нулю, так что начальное условие на бесконечности имеют вид:
h(r, t0) = 0; h(¥, t) = 0. (94)
Предположим далее, что расход закачиваемой жидкости изменяется со временем по степенному закону. Выражение для полного расхода жидкости, закачиваемой через скважину радиусом R, имеет вид:
|
(95)
По предположению, радиус скважины пренебрежимо мал (ниже мы остановимся на причинах, по которым это допущение можно делать для большинства реальных движений), поэтому можно принять R = 0; так как расход жидкости, закачиваемой в скважину, меняется по степенному закону, граничное, условие на скважине принимает вид:
|
(96)
|
|
(97)
Здесь
(98)
представляют собой две независимые безразмерные комбинации определяющих параметров решения; других независимых комбинаций этих параметров не существует. Постоянный множитель снова введен в формулу для x с целью удобства последующего изложения. Как и прежде, искомая функция должна быть непрерывной и иметь непрерывную производную от квадрата. Подставляя выражение (77) в уравнение (93) и условия (94) и (96), находим, что функция f1 (x, l) удовлетворяет уравнению
|
(99)
при условиях
|
(100)
Исследование этой граничной задачи проводится аналогично предыдущему; также единственным образом строится функция f1 (x, l), отличающаяся от нуля лишь при 0 £ x £ x1(l), где x1 (l) - некоторая функция x, а при x ³ x1 (l) тождественно равная нулю. Функция f1 (x, l) при x®0 имеет особенность, как нетрудно видеть из первого условия (100):
|
(101)
Второе условие (100) может быть приведено к другой форме: умножая уравнение (99) на x и интегрируя в пределах от x = 0 до x = ¥, получаем, используя оба условия (100) и условия
|
(102)
|
(103)
Первое условие (102) непосредственно следует из условия, которому функция f1 (x, l) на бесконечности, так как если бы предел == при x ® ¥ не был равен нулю, то функция f1 (x, l) не стремилась бы к нулю при x ® ¥. Второе условие (102) непосредственно следует из (101).
Эффективное вычисление функции f1 (x, l) удобно проводить следующим образом. Строим решение задачи Коши Ф1(x, l) для уравнения (99). обращающееся в нуль при x = 1 и имеющее в этой точке конечную первую производную. Исследование, в точности аналогичное приведенному в п. 3 x1, показывает, что эта производная равна -1/4. Строить решение задачи Коши удобно так: вблизи x = 1 можно представить решение в виде ряда, при помощи которого находится надлежащее число начальных значений, после чего применяется метод численного интегрирования Адамса - Штермера. Далее численно вычисляется величина
|
Величина N(l) не равна единице, поэтому функция, равная Ф1 (x, l) при x<1 и тождественно равная нулю при x ³ 1, удовлетворяет всем условиям граничной задачи (99) - (100), кроме первого условия (100). Воспользуемся теперь тем, что, как нетрудно показать, уравнение (99) и второе граничное условие (100) инвариантны относительно группы преобразований:
|
(104)
поэтому при произвольном положительном m функция Ф2(x, l) удовлетворяет уравнению (99) и второму граничному условию (100). Но
(105)
|
Выбрав ![]() так, что
так, что 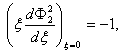
получим, что функция
|
(106)
удовлетво



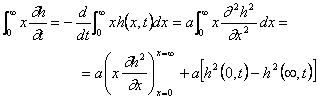 t5555555555
t5555555555